
科目: 来源: 题型:
【题目】福林制衣厂现有24名制作服装的工人,每天都制作某种品牌的衬衫和裤子,每人每天可制作这种衬衫3件或裤子5条.
(1)若该厂要求每天制作的衬衫和裤子数量相等,则应各安排多少人制作衬衫和裤子?
(2)已知制作一件衬衫可获得利润30元,制作一条裤子可获得利润16元,若该厂要求每天获得利润2100元,则需要安排多少名工人制作衬衫?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图:在数轴上 A 点表示数 a,B 点示数 b,C 点表示数 c,b 是最大的负整数,且 a、b 满足|a+ 3|+(c﹣6)2=0.
(1)a= ,b= ,c= ;
(2)若将数轴折叠,使得 A点与B 点重合,则点 C与数 表示的点重合;
(3)点 A、B、C开始在数轴上运动,若点 A以每秒 2个单位长度的速度向左运动,同时,点 B和 点 C分别以每秒1个单位长度和 4个单位长度的速度向右运动,假设 t 秒钟过后,若点 A与点 B之间的距离表示为 AB,点 A与点 C之间的距离表示为 AC,点 B与点 C之间的距离表示为 BC.则 AB= ,AC= ,BC= .(用 含 t的代数式表示)
(4)请问:2BC+AB - ![]() AC的值是否随着时间 t 的变化而改变?若变化,请说明理由;若不变,请求其值.
AC的值是否随着时间 t 的变化而改变?若变化,请说明理由;若不变,请求其值.
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】学习“利用三角函数测高”后,某综合实践活动小组实地测量了凤凰山与中心广场的相对高度AB,其测量步骤如下:
(1)在中心广场测点C处安置测倾器,测得此时山顶A的仰角∠AFH=30°;
(2)在测点C与山脚B之间的D处安置测倾器(C、D与B在同一直线上,且C、D之间的距离可以直接测得),测得此时山顶上红军亭顶部E的仰角∠EGH=45°;
(3)测得测倾器的高度CF=DG=1.5米,并测得CD之间的距离为288米;
已知红军亭高度为12米,请根据测量数据求出凤凰山与中心广场的相对高度AB.(![]() 取1.732,结果保留整数)
取1.732,结果保留整数)

查看答案和解析>>
科目: 来源: 题型:
【题目】一条小船沿直线向码头匀速前进.在0min ,2min,4min,6min时,测得小船与码头的距离分别为200m,150m,100m,50m.小船与码头的距离是时间的函数吗?如果是,写出函数的解析式,并画出函数图象.
查看答案和解析>>
科目: 来源: 题型:
【题目】某商场销售一种西装和领带,西装每套定价400元,领带每条定价50元.国庆节期间商场决定开展促销活动,活动期间向客户提供两种优惠方案, 两种优惠方案可以任意选择:方案一:买一套西装送一条领带;方案二:西装和领带都按定价的90%付款.
现某客户要到该商场购买西装20套,领带x![]() .
.
(1)若该客户按方案一购买,需付款 元(用含x的式子表示),
若该客户按方案二购买,需付款 元(用含x的式子表示)
(2)若![]() ,通过计算说明此时按哪种方案购买较为合算;
,通过计算说明此时按哪种方案购买较为合算;
(3)当![]() 时,你能给出一种更为省钱的购买方法吗?试写出你的购买方法和所需费用.
时,你能给出一种更为省钱的购买方法吗?试写出你的购买方法和所需费用.
查看答案和解析>>
科目: 来源: 题型:
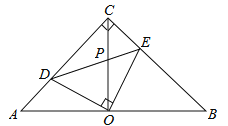
【题目】如图,在等腰直角△ACB中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P.则下列结论:
(1)图形中全等的三角形只有两对;
(2)△ABC的面积等于四边形CDOE的面积的2倍;
(3)CD+CE=![]() OA;
OA;
(4)AD2+BE2=2OPOC.其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线的一部分c1与经过点A、D、B的抛物线的一部分c2组合成一条封闭曲线,我们把这条封闭曲线成为“蛋线”.已知点C的坐标为(0,﹣![]() ),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.
),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.
(1)求A、B两点的坐标;
(2)“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由;
(3)当△BDM为直角三角形时,求m的值.

查看答案和解析>>
科目: 来源: 题型:
【题目】定义:数学活动课上,陈老师给出如下定义:有一组对边相等而另一组对边不相等的凸四边形叫做对等四边形.
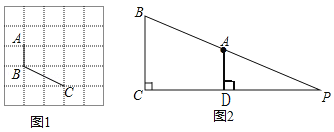
理解:(1)如图1,已知A、B、C在格点(小正方形的顶点)上,请在方格图中画出以格点为顶点,AB、BC为边的两个对等四边形ABCD;
应用:(2)如图2,在Rt△PBC中,∠PCB=90°,BC=9,点A在BP边上,且AB=13.AD⊥PC,CD=12,若PC上存在符合条件的点M,使四边形ABCM为对等四边形,求出CM的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com