
科目: 来源: 题型:
【题目】如图,△ABC中,D、E是BC边上的点,BD:DE:EC=3:2:1,M在AC边上,CM:MA=1:2,BM交AD,AE于H,G,则BH:HG:GM等于( )

A. 4:2:1 B. 5:3:1 C. 25:12:5 D. 51:24:10
查看答案和解析>>
科目: 来源: 题型:
【题目】某测量队在山脚A处测得山上树顶仰角为45°(如图),测量队在山坡上前进600米到D处,再测得树顶的仰角为60°,已知这段山坡的坡角为30°,如果树高为15米,则山高为( )(精确到1米, ![]() =1.732).
=1.732).

A. 585米 B. 1014米 C. 805米 D. 820米
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠C=90°,BC=CD=8,过点B作EB⊥AB,交CD于点E.若DE=6,则AD的长为( )

A.6 B.8 C.9 D.10
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,线段AB=10,射线BG⊥AB,P为射线BG上一点,以AP为边作正方形APCD,且C、D与点B在AP两侧,在线段DP取一点E,使∠EAP=∠BAP,直线CE与线段AB相交于点F(点F与点A、B不重合).
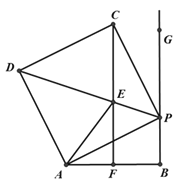
(1)求证:△AEP![]() △CEP;
△CEP;
(2)判断CF与AB的位置关系,并说明理由;
(3)求△AEF的周长
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像分别交于点A(2,m)、B(-4,-1),其中
的图像分别交于点A(2,m)、B(-4,-1),其中![]()
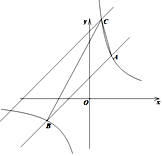
(1)求m的值和直线的解析式;
(2)若![]() ,观察图像,请直接写出x的取值范围;
,观察图像,请直接写出x的取值范围;
(3)将直线![]() 的图像向上平移与反比例函数的图像在第一象限内交于点C,C点的横坐标为1,
的图像向上平移与反比例函数的图像在第一象限内交于点C,C点的横坐标为1,
①判定△ABC的形状并说明理由,②求△ABC的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知抛物线y=![]() x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.

(1)求抛物线的解析式;(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】手工拉面是我国的传统美食.已知1根面条拉扣1次成2根.拉扣2次就成2x2根……每拉扣1次,面条数就增加1倍.
(1)设2位师傅各拿1根面条分别拉扣3次所成面条数之和为![]() ,3位师傅各拿1根面条分别拉扣2次所成面条数之和为
,3位师傅各拿1根面条分别拉扣2次所成面条数之和为![]() .试通过计算比较
.试通过计算比较![]() 的大小;
的大小;
(2)设张师傅在某次拉扣后所成面条的长度为0.8米/根,总长度为![]() 米,如果他又拉扣了2次,求此时面条增加了多少根?
米,如果他又拉扣了2次,求此时面条增加了多少根?
查看答案和解析>>
科目: 来源: 题型:
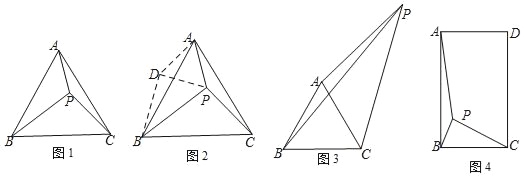
【题目】问题情境:如图1,在等边△ABC中,点P在△ABC内,且PA=3,PB=5,PC=4,求∠APC的度数?
小明在解决这个问题时,想到了以下思路:如图2,把△APC绕着点A顺时针旋转,使点C旋转到点B,得到△ADB,连结DP.
请你在小明的思路提示下,求出∠APC的度数.
思路应用:如图3,△ABC为等边三角形,点P在△ABC外,且PA=6,PC=8,∠APC=30°,求PB的长;
思路拓展:如图4,矩形ABCD中,AB=![]() BC,P为矩形ABCD内一点,PA:PB:PC=2
BC,P为矩形ABCD内一点,PA:PB:PC=2![]() :1:2,则∠APB= °.(直接填空)
:1:2,则∠APB= °.(直接填空)
查看答案和解析>>
科目: 来源: 题型:
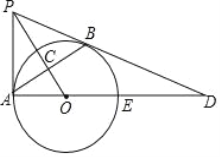
【题目】如图,PB与⊙O相切于点B,过点B作OP的垂线BA,垂足为C,交⊙O于点A,连结PA,AO,AO的延长线交⊙O于点E,与PB的延长线交于点D.
(1)求证:PA是⊙O的切线;
(2)若tan∠BAD=![]() ,且OC=4,求BD的长.
,且OC=4,求BD的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】我国是水资源比较贫乏的国家之一,为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段来达到节约用水的目的,规定如下用水收费标准:每户每月的用水不超过20立方米(含20立方米)时,水费按“基本价”收费:超过20立方米时,不超过的部分仍按“基本价”收费,超过部分按“调节价”收费.某户居民今年4、5月份的用水量和水费如下表所示:
月份 | 用水量(立方米) | 水费(元) |
4 | 20 | 42 |
5 | 24 | 56.40 |
(1)请你算一算该市水费的“调节价”每立方米多少元?
(2)若该户居民6月份用水量为30立方米,请算一算,6月份水费是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com