(1)用代数式表示:

①a与b的差的平方;②a与b两数平方和与a、b两数积的2倍的差;

(2)当a=3,b=-2时,求第(1)题中①②所列的代数式的值;

(3)由第(2)题的结果,你发现了什么等式?

(4)利用你发现的结论:求20182-4036×2017+20172的值.

【题目】已知抛物线．

（Ⅰ）若抛物线的顶点为（－2，－4），抛物线经过点（－4，0）．

①求该抛物线的解析式；

②连接，把所在直线沿轴向上平移，使它经过原点，得到直线，点是直线上一动点．

设以点， ， ， 为顶点的四边形的面积为，点的横坐标为，当≤≤时，求的取值范围；

（Ⅱ）若＞0， ＞1，当时， ，当0＜＜时， ＞0，试比较与1的大小，并说明理由．

【题目】在草莓上市的旺季，小颖和妈妈周末计划去草莓园采摘草莓.甲、乙两家草莓园生产的草莓品质相同，每千克售价均为元.甲草莓园的优惠方案是：游客进园需购买每人元的门票，采摘的草莓按六折收费；乙草莓园的优惠方案是：游客进园不需购买门票，采摘的草莓超过千克后，超过部分按五折收费.请你回答下列问题：

（1）如果去乙草莓园采摘千克草莓，需支付多少元？

（2）如果个人去甲草莓园采摘千克草莓，需支付多少元？

（3）小颖和妈妈准备采摘千克草莓送给朋友，哪家会更便宜？请说明理由.

【题目】随着互联网的发展，农副产品也可以网上销售经过一段时间的精准帮扶，小张也建起了自家的网络商店（简称网店），他应用网店将种植的苹果和桃子销往全国各地.其中苹果每箱个以上的公斤左右包邮元；桃子每箱个公斤左右包邮元.请你回答下列问题：

（1）网购一箱苹果和一箱桃子共应支付___________元；

（2）某社区重阳节慰问困难居民，计划在这家网店购买箱苹果和箱桃子，应支付的费用可表示为______________________元；

（3）因为水果不耐贮存，小丽和两个同学合起来在这家网店购买了两箱苹果和一箱桃子，然后平均分配，小丽需支付多钱？她可以分到几个苹果和几个桃子？请说明理由.

【题目】快递员小王下午骑摩托车从总部出发，在一条东西走向的街道上来回收送包裹.他行驶的情况记录如下（向东记为“”，向西记为“”，单位：千米）：

，，，，，，

（1）小王最后是否回到了总部？

（2）小王离总部最远是多少米？在总部的什么方向？

（3）如果小王每走米耗油毫升，那么小王下午骑摩托车一共耗油多少毫升？

【题目】如图，已知反比例函数的图像与一次函数的图像交于点，点．

（1）求k和b的值；

（2）连接OA、OB，求的面积；

（3）利用图像，直接写出时x的取值范围．

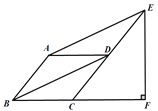
（1）求证：四边形ABCD是菱形；（2）若∠ABC＝45°，BC＝1，求EF的长.

（1）
（2）
（3）（）
（4）
（5）
（6）

【题目】在平面直角坐标系中，为坐标原点，点（0，1），点（1，0），正方形的两条对角线的交点为，延长至点，使．延长至点，使，以，为邻边做正方形．

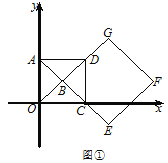
（Ⅰ）如图①，求的长及的值；

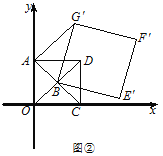
（Ⅱ）如图②，正方形固定，将正方形绕点逆时针旋转，得正方形，记旋转角为（0°＜＜360°），连接．

①旋转过程中，当90°时，求的大小；

②在旋转过程中，求的长取最大值时，点的坐标及此时的大小（直接写出结果即可）．

【题目】一位运动员推铅球，铅球运行时离地面的高度（米）是关于运行时间（秒）的二次函数．已知铅球刚出手时离地面的高度为米；铅球出手后，经过4秒到达离地面3米的高度，经过10秒落到地面．如图建立平面直角坐标系．

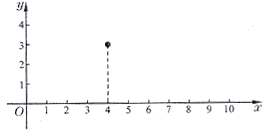
（Ⅰ）为了求这个二次函数的解析式，需要该二次函数图象上三个点的坐标．根据题意可知，该二次函数图象上三个点的坐标分别是____________________________；

（Ⅱ）求这个二次函数的解析式和自变量的取值范围．