
科目: 来源: 题型:
【题目】将五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和为( )
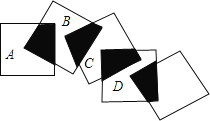
A.2cm2 B.4cm2 C.6cm2 D.8cm2
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,长方形纸片ABCD,点E,F分别在边AB,CD上,连接EF.将∠BEF对折,点B落在直线EF上的点B′处,得折痕EM;将∠AEF对折,点A落在直线EF上的点A′处,得折痕EN.
(1)判断直线EN,ME的位置关系,并说明理由;
(2)设∠MEN的平分线EP交边CD于点P,∠MEN的一条三等分线EQ交边CD于点Q.求∠PEQ的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E

(1)求证:DE=AB;
(2)以A为圆心,AB长为半径作圆弧交AF于点G,若BF=FC=1,求扇形ABG的面积.(结果保留π)
查看答案和解析>>
科目: 来源: 题型:
【题目】对于数据:80,88,85,85,83,83,84.下列说法中错误的有( )
A、这组数据的平均数是84;
B、这组数据的众数是85;
C、这组数据的中位数是84;
D、这组数据的方差是36.
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目: 来源: 题型:
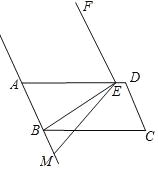
【题目】如图,四边形ABCD为平行四边形,过点B作BE⊥AB交AD于点E,将线段BE绕点E顺时针旋转90°到EF的位置,点M(点M不与点B重合)在直线AB上,连结EM.
(1)当点M在线段AB的延长线上时,将线段EM绕点E顺时针旋转90°到EN1的位置,连结FN1,在图中画出图形,求证:FN1⊥AB;
(2)当点M在线段BA的延长线上时,将线段EM绕点E顺时针旋转90°到EN2的位置,连结FN2,在图中画出图形,点N2在直线FN1上吗?请说明理由;
(3)若AB=3,AD=6,DE=1,设BM=x,在(1)、(2)的条件下,试用含x的代数式表示△FMN的面积.
查看答案和解析>>
科目: 来源: 题型:
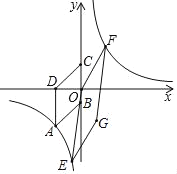
【题目】如图,在平面直角坐标系中,四边形ABCD为菱形,且点D(﹣4,0)在x轴上,点B和点C(0,3)在y轴上,反比例函数y=![]() (k≠0)过点A,点E(﹣2,m)、点F分别是反比例函数图象上的点,其中点F在第一象限,连结OE、OF,以线段OE、OF为邻边作平行四边形OEGF.
(k≠0)过点A,点E(﹣2,m)、点F分别是反比例函数图象上的点,其中点F在第一象限,连结OE、OF,以线段OE、OF为邻边作平行四边形OEGF.
(1)写出反比例函数的解析式;
(2)当点A、O、F在同一直线上时,求出点G的坐标;
(3)四边形OEGF周长是否有最小值?若存在,求出这个最值,并确定此时点F的坐标,若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
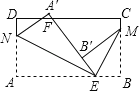
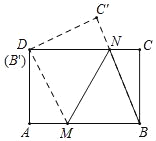
【题目】如图,四边形ABCD为矩形,将矩形ABCD沿MN折叠,折痕为MN,点B的对应点B′落在AD边上,已知AB=6,AD=4.
(1)若点B′与点D重合,连结DM,BN,求证:四边形BMB′N为菱形;
(2)在(1)问条件下求出折痕MN的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】计算或化简求值:
(1)(﹣2)2×5﹣(﹣2)3÷4;
(2)(﹣10)3+[(﹣4)2﹣(1﹣32)×2];
(3)求代数式3a+abc﹣![]() (9a﹣c2)的值,其中a=﹣
(9a﹣c2)的值,其中a=﹣![]() ,b=2,c=﹣3.
,b=2,c=﹣3.
(4)先化简再求值:![]() ,其中x=﹣2,y=
,其中x=﹣2,y=![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】为配合我市创建省级文明城市,某校对八年级各班文明行为劝导志愿者人数进行了统计,各班统计人数有6名、5名、4名、3名、2名、1名共计六种情况,并制作如下两幅不完整的统计图.
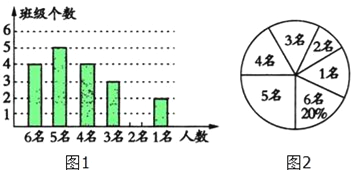
(1)求该年级平均每班有多少文明行为劝导志愿者?并将条形图补充完整;
(2)该校决定本周开展主题实践活动,从八年级只有2名文明行为劝导志愿者的班级中任选两名,请用列表或画树状图的方法,求出所选文明行为劝导志愿者有两名来自同一班级的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】数轴上原点左边有一点A,点A对应着数a,有如下说法:
①﹣a表示的数一定是一个正数.
②若|a|=9时,则a=﹣9.
③在﹣a,![]() ,a2,a3中,最大的数值是a2.
,a2,a3中,最大的数值是a2.
④式子|a+![]() |的最小值为2.
|的最小值为2.
其中正确的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com