
科目: 来源: 题型:
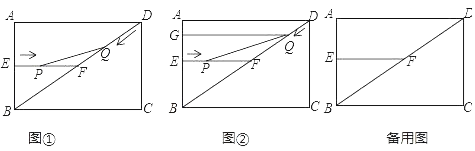
【题目】如图1,在矩形ABCD中,AB=6cm,BC=8cm,E、F分别是AB、BD的中点,连接EF,点P从点E出发,沿EF方向匀速运动,速度为1cm/s,同时,点Q从点D出发,沿DB方向匀速运动,速度为2cm/s,当点P停止运动时,点Q也停止运动.连接PQ,设运动时间为t(0<t<4)s,解答下列问题:
(1)求证:△BEF∽△DCB;
(2)当点Q在线段DF上运动时,若△PQF的面积为0.6cm2,求t的值;
(3)如图2过点Q作QG⊥AB,垂足为G,当t为何值时,四边形EPQG为矩形,请说明理由;
(4)当t为何值时,△PQF为等腰三角形?试说明理由.
查看答案和解析>>
科目: 来源: 题型:
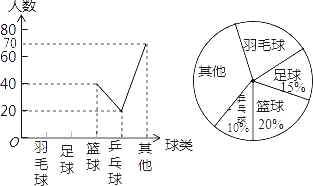
【题目】某中学在实施快乐大课间之前组织过“我最喜欢的球类”的调查活动,每个学生仅选择一项,通过对学生的随机抽样调查得到一组数据,如图是根据这组数据绘制成的不完整统计图.
(1)求出被调查的学生人数;
(2)把折线统计图补充完整;
(3)小亮、小莹、小芳和大刚到学校乒乓球室打乒乓球,当时只有一副空球桌,他们只能选两人打第一场.如果确定小亮打第一场,其余三人用“手心、手背”的方法确定谁获胜谁打第一场若三人中有一人出的与其余两人不同则获胜;若三人出的都相同则平局.已知大刚出手心,请用树状图分析大刚获胜的概率是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】“创卫工作人人参与,环境卫生人人受益”,我区创卫工作已进入攻坚阶段.某校拟整修学校食堂,现需购买A、B两种型号的防滑地砖共60块,已知A型号地砖每块80元,B型号地砖每块40元.
(1)若采购地砖的费用不超过3200元,那么,最多能购买A型号地砖多少块?
(2)某地砖供应商为了支持创卫工作,现将A、B两种型号的地砖单价都降低a%,这样,该校花费了2560元就购得所需地砖,其中A型号地砖a块,求a的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合.将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q.
(1)如图①,当点Q在线段AC上,且AP=AQ时,求证:△BPE≌△CQE;
(2)如图②,当点Q在线段CA的延长线上时,求证:△BPE∽△CEQ;并求当BP=a,CQ=![]() a 时,P、Q两点间的距离 (用含a的代数式表示).
a 时,P、Q两点间的距离 (用含a的代数式表示).

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在对Rt△OAB依次进行位似、轴对称和平移变换后得到△O′A′B′.
(1)在坐标纸上画出这几次变换相应的图形;
(2)设P(x,y)为△OAB边上任一点,依次写出这几次变换后点P对应点的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下列短文,并回答下列问题:我们把相似的概念推广到空间:如果两个几何体大小不一定相等,但形状完全相同,我们就把它们叫作相似体.
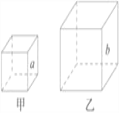
如图,甲、乙是两个不同的正方体,正方体都是相似体,它们的一切对应线段之比都等于相似比( a ∶ b ),设S 甲 ,S 乙 分别表示这两个正方体的表面积,则![]()
.又设V 甲 ,V 乙 分别表示这两个正方体的体积,则![]() .
.
(1)下列几何体中,一定属于相似体的是(___)
A.两个球体 B.两个圆锥体
C.两个圆柱体 D.两个长方体
(2)请归纳出相似体的三个主要性质:①相似体的一切对应线段(或弧)的比等于__________;②相似体的表面积的比等于__________;③相似体的体积比等于__________.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:Rt△A′BC′≌Rt△ABC,∠A′C′B=∠ACB=90°,∠A′BC′=∠ABC=60°,Rt△A′BC′可绕点B旋转,设旋转过程中直线CC′和AA′相交于点D.
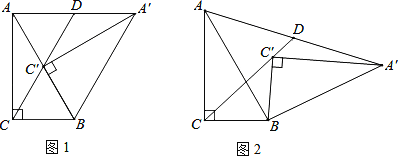
(1)如图1所示,当点C′在AB边上时,判断线段AD和线段A′D之间的数量关系,并证明你的结论;
(2)将Rt△A′BC′由图1的位置旋转到图2的位置时,(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由;
(3)将Rt△A′BC′由图1的位置按顺时针方向旋转α角(0°≤α≤120°),当A、C′、A′三点在一条直线上时,请直接写出旋转角的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°∠ACB=60°.将Rt△ABC绕点C顺时针方向旋转后得到△DEC(△DEC≌△ABC),点E在AC上,再将Rt△ABC沿着AB所在直线翻转180°得到△ABF,连接AD.

(1)求证:四边形AFCD是菱形;
(2)连接BE并延长交AD于点G,连接CG.请问:四边形ABCG是什么特殊平行四边形?为什么?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在梯形ABCD中,已知AD∥BC,AB=DC,AD=2,BC=4,延长BC到E,使CE=AD.
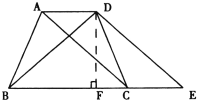
(1)写出图中所有与△DCE全等的三角形,并选择其中一对说明全等的理由;
(2)探究:当梯形ABCD的高DF等于多少时,对角线AC与BD互相垂直?请回答并说明理由.
查看答案和解析>>
科目: 来源: 题型:
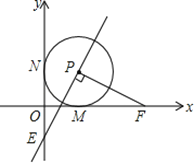
【题目】已知在平面直角坐标系xOy中,O是坐标原点,以P(1,1)为圆心的⊙P与x轴、y轴分别相切于点M和点N,点F从点M出发,沿x轴正方向以每秒1个单位长度的速度运动,连接PF,过点P作PE⊥PF交y轴于点E,设点F运动的时间是t秒(t>0)
(1)若点E在y轴的负半轴上(如图所示),求证:PE=PF;
(2)在点F运动过程中,设OE=a,OF=b,试用含a的代数式表示b;
(3)作点F关于点M的对称点F′,经过M、E和F′三点的抛物线的对称轴交x轴于点Q,连接QE.在点F运动过程中,是否存在某一时刻,使得以点Q、O、E为顶点的三角形与以点P、M、F为顶点的三角形相似?若存在,请直接写出t的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com