
科目: 来源: 题型:
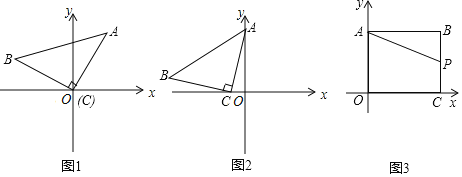
【题目】![]() 操作思考:如图1,在平面直角坐标系中,等腰
操作思考:如图1,在平面直角坐标系中,等腰![]() 的直角顶点C在原点,将其绕着点O旋转,若顶点A恰好落在点
的直角顶点C在原点,将其绕着点O旋转,若顶点A恰好落在点![]() 处
处![]() 则
则![]() 的长为______;
的长为______;![]() 点B的坐标为______
点B的坐标为______![]() 直接写结果
直接写结果![]()
![]() 感悟应用:如图2,在平面直角坐标系中,将等腰
感悟应用:如图2,在平面直角坐标系中,将等腰![]() 如图放置,直角顶点
如图放置,直角顶点![]() ,点
,点![]() ,试求直线AB的函数表达式.
,试求直线AB的函数表达式.
![]() 拓展研究:如图3,在直角坐标系中,点
拓展研究:如图3,在直角坐标系中,点![]() ,过点B作
,过点B作![]() 轴,垂足为点A,作
轴,垂足为点A,作![]() 轴,垂足为点C,P是线段BC上的一个动点,点Q是直线
轴,垂足为点C,P是线段BC上的一个动点,点Q是直线![]() 上一动点
上一动点![]() 问是否存在以点P为直角顶点的等腰
问是否存在以点P为直角顶点的等腰![]() ,若存在,请求出此时P的坐标,若不存在,请说明理由.
,若存在,请求出此时P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
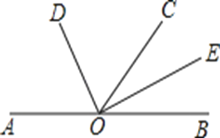
【题目】如图,已知A,O,B三点在同一条直线上,OD平分∠AOC,OE平分∠BOC.
(1)若∠BOC=62°,求∠DOE的度数;
(2)若∠BOC=α,求∠DOE的度数;
(3)通过(1)(2)的计算,你能总结出什么结论,直接简写出来,不用说明理由.
查看答案和解析>>
科目: 来源: 题型:
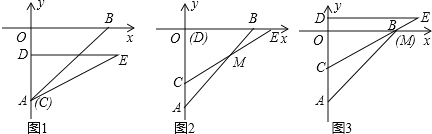
【题目】已知:如图,一块Rt△ABC的绿地,量得两直角边AC=8cm,BC=6cm.现在要将这块绿地扩充成等腰△ABD,且扩充部分(△ADC)是以8cm为直角边长的直角三角形,求扩充等腰△ABD的周长.
(1)在图1中,当AB=AD=10cm时,△ABD的周长为 .
(2)在图2中,当BA=BD=10cm时,△ABD的周长为 .
(3)在图3中,当DA=DB时,求△ABD的周长.

查看答案和解析>>
科目: 来源: 题型:
【题目】解方程:
(1)(x-5)2=16 (直接开平方法) (2)x2+5x=0 (因式分解法)
(3)x2-4x+1=0 (配方法) (4)x2+3x-4=0 (公式法)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图A在数轴上对应的数为-2.
(1)点B在点A右边距离A点4个单位长度,则点B所对应的数是_____.
(2)在(1)的条件下,点A以每秒2个单位长度沿数轴向左运动,点B以每秒3个单位长度沿数轴向右运动.现两点同时运动,当点A运动到-6的点处时,求A、B两点间的距离.
(3)在(2)的条件下,现A点静止不动,B点以原速沿数轴向左运动,经过多长时间A、B两点相距4个单位长度.
![]()
查看答案和解析>>
科目: 来源: 题型:
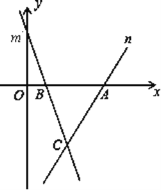
【题目】如图,直线m的表达式为y =﹣3x+3,且与x轴交于点B,直线n经过点A(4,0),且与直线m交于点C(t,﹣3)
(1)求直线n的表达式.
(2)求△ABC的面积.
(3)在直线n上存在异于点C的另一点P,使△ABP与△ABC的面积相等,请直接写出点P的坐标是 .
查看答案和解析>>
科目: 来源: 题型:
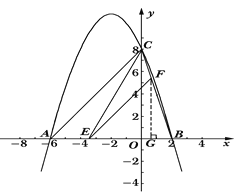
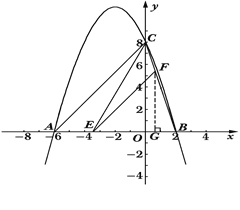
【题目】已知:二次函数![]() 的图象与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x2-10x+16=0的两个根,且A点坐标为(-6,0).
的图象与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x2-10x+16=0的两个根,且A点坐标为(-6,0).
(1)求此二次函数的表达式;
(2)若点E是线段AB上的一个动点(与点A、点B不重合),过点E作EF∥AC交BC于点F,连接CE,设AE的长为m,△CEF的面积为S,求S与m之间的函数关系式,并写出自变量m的取值范围;
【答案】(1)y=-![]() x2-
x2-![]() x+8(2)
x+8(2)
【解析】试题分析:(1)求出一元二次方程的两根即可求出两点坐标,把B、C两点坐标代入二次函数的解析式就可解答;
(2)过点F作FG⊥AB,垂足为G,由EF∥AC,得△BEF∽△BAC,利用相似比求EF,利用sin∠FEG=sin∠CAB求FG,根据S=S△BCE-S△BFE,求S与m之间的函数关系式.
解:(1)解方程x2-10x+16=0得x1=2,x2=8
∴B(2,0)、C(0,8)
∴所求二次函数的表达式为y=-![]() x2-
x2-![]() x+8
x+8
(2)∵AB=8,OC=8,依题意,AE=m,则BE=8-m,
∵OA=6,OC=8, ∴AC=10.
∵EF∥AC, ∴△BEF∽△BAC.
∴![]() =
=![]() . 即
. 即![]() =
=![]() . ∴EF=
. ∴EF=![]() .
.
过点F作FG⊥AB,垂足为G,
则sin∠FEG=sin∠CAB=![]() .∴
.∴![]() =
=![]() .
.
∴FG=![]() ·
·![]() =8-m.
=8-m.
∴S=S△BCE-S△BFE
=![]()
![]() (0<m<8)
(0<m<8)
点睛:本题考查了一元二次方程的解法,待定系数法求函数关系系,相似三角形的判定与性质,span>锐角三角函数的定义,割补法求图形的面积,熟练掌握待定系数法求二次函数关系式、相似三角形的判定与性质是解答本题的关键.
【题型】解答题
【结束】
23
【题目】如图(1),在平面直角坐标系中,点A(0,﹣6),点B(6,0).Rt△CDE中,∠CDE=90°,CD=4,DE=4![]() ,直角边CD在y轴上,且点C与点A重合.Rt△CDE沿y轴正方向平行移动,当点C运动到点O时停止运动.解答下列问题:
,直角边CD在y轴上,且点C与点A重合.Rt△CDE沿y轴正方向平行移动,当点C运动到点O时停止运动.解答下列问题:
(1)如图(2),当Rt△CDE运动到点D与点O重合时,设CE交AB于点M,求∠BME的度数.
(2)如图(3),在Rt△CDE的运动过程中,当CE经过点B时,求BC的长.
(3)在Rt△CDE的运动过程中,设AC=h,△OAB与△CDE的重叠部分的面积为S,请写出S与h之间的函数关系式,并求出面积S的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】几何计算:
如图,已知∠AOB=40°,∠BOC=3∠AOB,OD平分∠AOC,求∠COD的度数.
解:因为∠BOC=3∠AOB,∠AOB=40°
所以∠BOC=__________°
所以∠AOC=__________ + _________
=__________° + __________°
=__________°
因为OD平分∠AOC
所以∠COD=![]() __________=__________°
__________=__________°

查看答案和解析>>
科目: 来源: 题型:
【题目】在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上,请解答下列问题:

(1)①作出△ABC向左平移4个单位长度后得到的△A1B1C1, 并写出点C1的坐标;
②作出△ABC关于原点O对称的△A2B2C2, 并写出点C2的坐标;
(2)已知△ABC关于直线l对称的△A3B3C3的顶点A3的坐标为(-4,-2),请直接写出直线l的函数解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com