
科目: 来源: 题型:
【题目】如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD的长为x,四边形ABCD的面积为y,则y与x之间的函数关系式是( )

A. y=![]() B. y=
B. y=![]() C. y=
C. y=![]() D. y=
D. y=![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K﹣∠H=27°,则∠K=( )

A. 76° B. 78° C. 80° D. 82°
查看答案和解析>>
科目: 来源: 题型:
【题目】在矩形ABCD中,∠B的角平分线BE与AD交于点E,∠BED的角平分线EF与DC交于点F,若AB=9,DF=2FC,则BC=____.(结果保留根号)

查看答案和解析>>
科目: 来源: 题型:
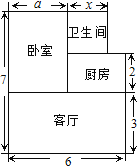
【题目】张先生准备在沙坪坝购买一套小户型商品房,他去某楼盘了解情况得知,该户型商品房的单价是12000元/m2,面积如图所示(单位:米,卧室的宽为a米,卫生间的宽为x米),
(1) 用含a和x的式子表示该户型的面积
(2) 售房部为张先生提供了以下两种优惠方案:
方案一:整套房的单价是12 000元/m2,其中厨房只算![]() 的面积;
的面积;
方案二:整套房按原销售总金额的9折出售,
若张先生购买的户型a=3,且分别用两种方案购房金额相等,求x的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】十八世纪瑞士数学家欧拉证明了简单多面体中项点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式。请你观察下列儿种简单多面体模型,解答下列问题:

(1)根据上面多面体模型,完成表格中的空格:
多面体 | 项点数(V) | 面数(F) | 棱数(F) |
四面体 | |||
长方体 | |||
正八面体 | |||
正十二面体 |
你发现项点数(V)、面数(F)、棱数(F)之间存在的关系式是__________________________.
(2)一个多面体的面数比顶点数小8,且有30条棱,则这多面体的顶点数是 20;
(3)某个玻璃饰品的外形是简单多面体,它的外表是由三角形和八边形两种多边形拼接而成,且有48个顶点,每个顶点处都有3条棱,设该多面体表面三角形的个数为x个,八边形的个数为y个,求x+y的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在直角墙角AOB(OA⊥OB,且OA、OB长度不限)中,要砌20m长的墙,与直角墙角AOB围成地面为矩形的储仓,且地面矩形AOBC的面积为96m2.
(1)求地面矩形AOBC的长;
(2)有规格为0.80×0.80和1.00×1.00(单位:m)的地板砖单价分别为55元/块和80元/块,若只选其中一种地板砖都恰好能铺满储仓的矩形地面(不计缝隙),用哪一种规格的地板砖费用较少?

查看答案和解析>>
科目: 来源: 题型:
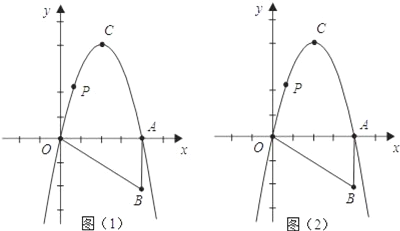
【题目】如图,Rt△OAB如图所示放置在平面直角坐标系中,直角边OA与x轴重合,∠OAB=90°,OA=4,AB=2,把Rt△OAB绕点O逆时针旋转90°,点B旋转到点C的位置,一条抛物线正好经过点O,C,A三点.
(1)求该抛物线的解析式;
(2)在x轴上方的抛物线上有一动点P,过点P作x轴的平行线交抛物线于点M,分别过点P,点M作x轴的垂线,交x轴于E,F两点,问:四边形PEFM的周长是否有最大值?如果有,请求出最值,并写出解答过程;如果没有,请说明理由.
(3)如果x轴上有一动点H,在抛物线上是否存在点N,使O(原点)、C、H、N四点构成以OC为一边的平行四边形?若存在,求出N点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,在菱形ABCD中,点E,O,F分别为AB,AC,AD的中点,连接CE,CF,OE,OF.
(1)求证:△BCE≌△DCF;
(2)当AB与BC满足什么关系时,四边形AEOF是正方形?请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知:b是最小的正整数,且a、b满足(c﹣6)2+|a+b|=0,请回答问题
(1)请直接写出a、b、c的值.a= ,b= ,c=
(2)a、b、c所对应的点分别为A、B、C,点P为一动点,其对应的数为x,点P在A、B之间运动时,请化简式子:|x+1|﹣|x﹣1|﹣2|x+5|(请写出化简过程)
![]()
(3)在(1)(2)的条件下,点A、B、C开始在数轴上运动,若点A以每秒n(n>0)个单位长度的速度向左运动,同时,点B和点C分别以每秒2n个单位长度和5n个单位长度的速度向右运动,假设经过t秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB.请问:BC﹣AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.
查看答案和解析>>
科目: 来源: 题型:
【题目】超速行驶是引发交通事故的主要原因之一.上周末,小明和三位同学尝试用自己所学的知识检测车速.如图,观测点设在A处,离益阳大道的距离(AC)为30米.这时,一辆小轿车由西向东匀速行驶,测得此车从B处行驶到C处所用的时间为8秒,∠BAC=75°.
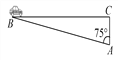
(1)求B、C两点的距离;
(2)请判断此车是否超过了益阳大道60千米/小时的限制速度?
(计算时距离精确到1米,参考数据:sin75°≈0.9659,cos75°≈0.2588,tan75°≈3.732, ![]() ≈1.732,60千米/小时≈16.7米/秒)
≈1.732,60千米/小时≈16.7米/秒)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com