
科目: 来源: 题型:
【题目】(1)如图1,小明同学在某月的日历上圈出![]() 个数,正方形的方框内的4个数的和是32,那么第1个数
个数,正方形的方框内的4个数的和是32,那么第1个数![]() 是.
是.
(2)如图2,玛丽也在上面的日历上圈出![]() 个数,斜框内的4个数的和是__________(用含
个数,斜框内的4个数的和是__________(用含![]() 的代数式表示);
的代数式表示);

(3)某月有5个星期日的和是75,则这个月中最后1个星期日是__________号;
(4)变式拓展:
若干个偶数按每行8个数排成如图:
①如图①,长方形方框内的9个数的和为__________.
②如图②,小丽所画的斜框内9个数,若它们的和为![]() ,则中间的数△为__________(用含
,则中间的数△为__________(用含![]() 的代数式表示).
的代数式表示).

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知正方形ABCD的对角线交于O点,点E,F分别是AO,CO的中点,连接BE,BF,DE,DF,则下列结论中一定成立的是________.(把所有正确结论的序号都填在横线上)
①BF=DE;②∠ABO=2∠ABE;③S△AED=![]() S△ACD;④四边形BFDE是菱形.
S△ACD;④四边形BFDE是菱形.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正方形A1A2A3A4,A5A6A7A8,A9A10A11A12,…(每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为A1,A2,A3,A4;A5,A6,A7,A8;A9,A10,A11,A12;…)的中心均在坐标原点O,各边均与x轴或y轴平行,若它们的边长依次是2,4,6,…,则顶点A20的坐标为 ( )
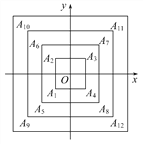
A. (5,5) B. (5,-5) C. (-5,5) D. (-5,-5)
查看答案和解析>>
科目: 来源: 题型:
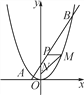
【题目】如图,已知一条直线过点(0,4),且与抛物线y=![]() x2交于A,B两点,其中点A的横坐标是-2.
x2交于A,B两点,其中点A的横坐标是-2.
(1)求这条直线的解析式及点B的坐标;
(2)在x轴上是否存在点C,使得△ABC是直角三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)过线段AB上一点P,作PM∥x轴,交抛物线于点M,点M在第一象限,点N(0,1),当点M的横坐标为何值时,MN+3MP的长度最大?最大值是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】小虫从![]() 点出发在一条直线上来回爬行,假定向右爬行的路程记作正数,向左爬行的路程记作负数,爬行的各段路程(单位:
点出发在一条直线上来回爬行,假定向右爬行的路程记作正数,向左爬行的路程记作负数,爬行的各段路程(单位:![]() )依次为:
)依次为:![]() .
.
(1)小虫在爬行过程中离![]() 点最远的距离是多少?
点最远的距离是多少?
(2)小虫爬到最后距![]() 点多远?
点多远?
(3)如果小虫爬行![]() 就奖励它一粒芝麻,那么小虫一共可得到多少粒芝麻?
就奖励它一粒芝麻,那么小虫一共可得到多少粒芝麻?
查看答案和解析>>
科目: 来源: 题型:
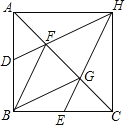
【题目】已知:如图,在△ABC中,AB=BC,∠ABC=90°,点D、E分别是边AB、BC的中点,点F、G是边AC的三等分点,DF、EG的延长线相交于点H,连接HA、HC.
(1)求证:四边形FBGH是菱形;
(2)求证:四边形ABCH是正方形.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)、求证:四边形AODE是矩形;(2)、若AB=6,∠BCD=120°,求四边形AODE的面积.

查看答案和解析>>
科目: 来源: 题型:
【题目】(2014四川资阳)如图①,已知直线l1∥l2,线段AB在直线l1上,BC垂直于l1交l2于点C,且AB=BC,P是线段BC上异于两端点的一点,过点P的直线分别交l2,l1于点D,E(点A,E位于点B的两侧,满足BP=BE,连接AP,CE.
(1)求证:△ABP≌△CBE.
(2)连接AD、BD,BD与AP相交于点F,如图②.
①当![]() 时,求证:AP⊥BD;
时,求证:AP⊥BD;
②当![]() (n>1)时,设△PAD的面积为S1,△PCE的面积为S2,求
(n>1)时,设△PAD的面积为S1,△PCE的面积为S2,求![]() 的值.
的值.

查看答案和解析>>
科目: 来源: 题型:
【题目】为鼓励节约用水,某地推行阶梯式水价计费制,标准如下:每月用水不超过17立方米的按每立方米![]() 元计费,超过17立方米而未超过30立方米的部分按每立方米
元计费,超过17立方米而未超过30立方米的部分按每立方米![]() 元计费,超过30立方米的部分按每立方米
元计费,超过30立方米的部分按每立方米![]() 元计费,某户居民上月用水35立方米,应缴水费_________元.
元计费,某户居民上月用水35立方米,应缴水费_________元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com