
科目: 来源: 题型:
【题目】如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接EF.给出下列五个结论:①AP=EF;②AP⊥EF;③△APD一定是等腰三角形;④∠PFE=∠BAP;⑤PD=![]() EC.其中正确结论的序号是( )
EC.其中正确结论的序号是( )
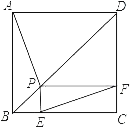
A. ①②③④B. ①②④⑤C. ②③④⑤D. ①③④⑤
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1所示,在正方形ABCD和正方形CGEF中,点B、C、G在同一条直线上,M是线段AE的中点,DM的延长线交EF于点N,连接FM,易证:DM=FM,DM⊥FM(无需写证明过程)
(1)如图2,当点B、C、F在同一条直线上,DM的延长线交EG于点N,其余条件不变,试探究线段DM与FM有怎样的关系?请写出猜想,并给予证明;
(2)如图3,当点E、B、C在同一条直线上,DM的延长线交CE的延长线于点N,其余条件不变,探究线段DM与FM有怎样的关系?请直接写出猜想.

查看答案和解析>>
科目: 来源: 题型:
【题目】蜜蜂是自然界神奇的“建筑师“,它能用最少的材料造成最牢固的建筑物“蜂窝“,观察下列的“蜂窝图
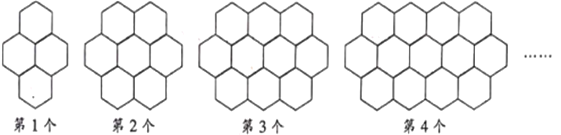
(1)若“![]() ”中每条边看成1个建筑单位,则第1个图形中共有19个建筑单位,第2个图案中共有_____个建筑单位;第3个图案中共有_____个建筑单位.
”中每条边看成1个建筑单位,则第1个图形中共有19个建筑单位,第2个图案中共有_____个建筑单位;第3个图案中共有_____个建筑单位.
(2)第n个图案中共有多少个建筑单位.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,E为垂足,连结DF,则∠CDF等于( )

A. 80° B. 70° C. 65° D. 60°
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=6cm,BC=12cm.∠B=30°.点P在BC上由点B向点C出发,速度为每秒2cm;点Q在边AD上,同时由点D向点A运动,速度为每秒1cm,当点P运动到点C时,P、Q同时停止运动.连接PQ,设运动时间为t秒.
(1)当t为何值时四边形ABPQ为平行四边形?
(2)设四边形ABPQ的面积为y,求y与t之间的函数关系式.
(3)当t为何值时,四边形ABPQ的面积是四边形ABCD的面积的四分之三,并求出此时∠PQD的度数.
(4)连结AP,是否存在某一时刻t,使△ABP为等腰三角形?并求出此刻t的值.

查看答案和解析>>
科目: 来源: 题型:
【题目】桐城市发起了“保护龙眠河”行动,某学校七年级两个班的115名学生积极参与,踊跃捐款,已知甲班有![]() 的学生每人捐了10元,乙班有
的学生每人捐了10元,乙班有![]() 的学生每人捐了10元,两个班其余学生每人捐了5元,设甲班有学生x人。
的学生每人捐了10元,两个班其余学生每人捐了5元,设甲班有学生x人。
(1)用含x的代数式表示乙班人数: ;
(2)用含x的代数式表示两班捐款的总额;
(3)若x=60,则两班共捐款多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】星光中学课外活动小组准备围建一个矩形生物苗圃园,其中一边靠墙,另外三边用长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边的长为x米.
(1)若平行于墙的一边长为y米,直接写出y与x的函数关系式及其自变量x的取值范围;
(2)垂直于墙的一边的长为多少米时,这个苗圃园的面积最大,并求出这个最大值;
(3)当这个苗圃园的面积不小于88平方米时,试结合函数图象,直接写出x的取值范围.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,将四张边长各不相同的正方形纸片按如图方式放入矩形ABCD内(相邻纸片之间互不重叠也无缝隙),未被四张正方形纸片覆盖的部分用阴影表示,设右上角与左下角阴影部分的周长的差为l.若知道l的值,则不需要测量就能知道周长的正方形的标号为( )

A.①B.②C.③D.④
查看答案和解析>>
科目: 来源: 题型:
【题目】数学问题:计算等差数列5,2,﹣1,﹣4……前n项的和.
问题探究:为解决上面的问题,我们从最简单的问题进行探究.
探究一:首先我们来认识什么是等差数列.
数学上,称按一定顺序排列的一列数为数列,其中排在第一位的数称为第1项,用a1表示:排在第二位的数称为第2项,用a2表示……排在第n位的数称为第n项,用an表示.一般地,如果一个数列从第二项起,每一项与它的前一项的差都等于同一个常数,那么这个数列叫做等差数列,这个常数叫等差数列的公差,公差通常用字母d表示.如:数列2,4,6,8,….为等差数列,其中a1=2,公差d=2.
(1)已知等差数列5,2,﹣1,﹣4,…则这个数列的公差d= ,第5项是 .
(2)如果一个数列a1,a2,a3,a4,…是等差数列,且公差为d,那么根据定义可得到:
a2﹣a1=d,a3﹣a2=d,a4﹣a3=d,……an﹣an﹣1=d,所以a2=a1+d,a3=a2+d=a1+2d,a4=a1+3d,……:由此可得an= (用a1和d的代数式表示)
(3)对于等差数列5,2,﹣1,﹣4,…,an= 请判断﹣2020是否是此等差数列的某一项,若是,请求出是第几项:若不是,说明理由.
探究二:二百多年前,数学王子高斯用他独特的方法快速计算出1+2+3+4+…+100的值.我们从这个算法中受到启发,用此方法计算数列1,2,3,…,n的前n项和:由 可知
可知![]()
(4)请你仿照上面的探究方式,解决下面的问题:
若a1,a2,a3,…,an为等差数列的前n项,前n项和Sn=a1+a2+a3+…+an.证明:Sn=na1+![]() .
.
(5)计算:计算等差数列5,2,﹣1,﹣4…前n项的和Sn(写出计算过程).
查看答案和解析>>
科目: 来源: 题型:
【题目】实践探究题
(1)观察下列有规律的数:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() …根据规律可知
…根据规律可知
①第10个数是________; ![]() 是第________个数.
是第________个数.
②计算![]() ________.(直接写出答案即可)
________.(直接写出答案即可)
(2)![]() 是不为1的有理数,我们把
是不为1的有理数,我们把![]() 称为
称为![]() 的差倒数.如:2的差倒数是
的差倒数.如:2的差倒数是![]() ,
,![]() 的差倒数是
的差倒数是![]() .已知
.已知![]() ,
,![]() 是
是![]() 的差倒数,
的差倒数,![]() 是
是![]() 的差倒数,
的差倒数,![]() 是
是![]() 的差倒数,…,依此类推,
的差倒数,…,依此类推,![]() 是
是![]() 的差倒数,则
的差倒数,则![]() ________.
________.
(3)高斯函数[x],也称为取整函数,即[x]表示不超过x的最大整数.
例如:[2.3]=2,[-1.5]=-2.则下列结论:①[-2.1]+[1]=-2; ②[x]+[-x]=0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com