
科目: 来源: 题型:
【题目】如图,四边形ABCD中,AD∥BC,∠ABC=90°.
(1)直接填空:∠BAD=______°.
(2)点P在CD上,连结AP,AM平分∠DAP,AN平分∠PAB,AM、AN分别与射线BP交于点M、N.设∠DAM=α°.
①求∠BAN的度数(用含α的代数式表示).
②若AN⊥BM,试探究∠AMB的度数是否为定值?若为定值,请求出该定值;若不为定值,请用α的代数式表示它.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1) 请画出△ABC向左平移5个单位长度后得到的△A![]() B
B![]() C
C![]() ;
;
(2) 请画出△ABC关于原点对称的△A![]() B
B![]() C
C![]() ;
;
(3) 在![]() 轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】某手机经销商计划同时购进一批甲、乙两种型号的手机,已知每部甲种型号的手机进价比每部乙种型号的手机进价多200元,且购进3部甲型号手机和2部乙型号手机,共需要资金9600元;
(1)求甲、乙型号手机每部进价为多少元?
(2)该店计划购进甲、乙两种型号的手机共20台进行销售,现已有顾客预定了8台甲种型号手机,且该店投入购进手机的资金不多于3.8万元,请求出有几种进货方案?并请写出进货方案.
(3)售出一部甲种型号手机,利润率为30%,乙种型号手机的售价为2520元.为了促销,公司决定每售出一台乙型号手机,返还顾客现金m元充话费,而甲型号手机售价不变,要使(2)中所有方案获利相同,求m的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某商品的进货价为每件30元,为了合理定价,先投放市场试销.据市场调查,销售价为每件40元时,每周的销售量是180件,而销售价每上涨1元,则每周的销售量就会减少5件,设每件商品的销售价上涨x元,每周的销售利润为y元.
(1)用含x的代数式表示:每件商品的销售价为 元,每件商品的利润为 元,每周的商品销售量为 件;
(2)求y关于x的函数关系式(不要求写出x的取值范围);
(3)应怎样确定销售价,使该商品的每周销售利润最大?最大利润是多少?
查看答案和解析>>
科目: 来源: 题型:
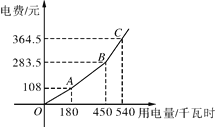
【题目】为了响应国家节能减排的号召,鼓励市民节约用电,我市从2012年7月1日起,居民用电实行“一户一表”的“阶梯电价”,分三个档次收费,第一档是用电量不超过180千瓦时实行“基本电价”,第二、三档实行“提高电价”,具体收费情况如图的折线图,请根据图象回答下列问题;
(1)当用电量是180千瓦时时,电费是__________元;
(2)第二档的用电量范围是__________;
(3)“基本电价”是__________元/千瓦时;
(4)小明家8月份的电费是328.5元,这个月他家用电多少千瓦时?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点E是正方形ABCD的边AB上一点,将△DAE逆时针旋转后能够与△DCF重合.
(1)旋转中心是______,旋转角的度数为______°.
(2)若∠DFB=65°,求∠DEB的度数.
(3)若AD=5,AE=m,求四边形DEBF的面积.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知正比例函数![]() 与反比例函数
与反比例函数![]() .
.
(1)证明:直线与双曲线没有交点;
(2)若将直线![]() 向上平移4个单位后与双曲线恰好有且只有一个交点,求反比例函数的表达式和平移后的直线表达式;
向上平移4个单位后与双曲线恰好有且只有一个交点,求反比例函数的表达式和平移后的直线表达式;
(3)将(2)小题平移后的直线代表的函数记为![]() ,根据图象直接写出:对于负实数
,根据图象直接写出:对于负实数![]() ,当
,当![]() 取何值时
取何值时![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校准备印刷一批证书,现有两个印刷厂可供选择:甲厂收费方式:收制版费1000元,每本印刷费0.5元;乙厂收费方式:不收制版费,每本收印刷费1.5元;若该校印制证书x本.
(1)当印制证书3000本时,甲厂的收费为 元,乙厂的收费为 元;
(2)请问印刷多少本证书时,甲乙两厂收费相同?
(3)你认为选择哪一家印刷厂更优惠?
查看答案和解析>>
科目: 来源: 题型:
【题目】在数学拓展课上,老师让同学们探讨特殊四边形的做法:
如图,先作线段![]() ,作射线
,作射线![]() (
(![]() 为锐角),过
为锐角),过![]() 作射线
作射线![]() 平行于
平行于![]() ,再作
,再作![]() 和
和![]() 的平分线分别交
的平分线分别交![]() 和
和![]() 于点
于点![]() 和
和![]() ,连接
,连接![]() ,则四边形
,则四边形![]() 为菱形;
为菱形;
(1)你认为该作法正确吗?请说明理由.
(2)若![]() ,并且四边形
,并且四边形![]() 的面积为
的面积为![]() ,在
,在![]() 上取一点
上取一点![]() ,使得
,使得![]() .请问图中存在这样的点
.请问图中存在这样的点![]() 吗?若存在,则求出
吗?若存在,则求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】把一个足球垂直地面向上踢,![]() (秒)后该足球的高度
(秒)后该足球的高度![]() (米)适用公式
(米)适用公式![]() .
.
(1)经多少秒时足球的高度为20米?
(2)小明同学说:“足球高度不可能达到21米!”你认为他说得对吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com