
科目: 来源: 题型:
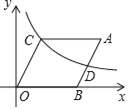
【题目】如图,ABOC放置在直角坐标系中,点A(10,4),点B(6,0),反比例函数y=![]() (x>0)的图象经过点C.
(x>0)的图象经过点C.
(1)求该反比例函数的表达式.
(2)记AB的中点为D,请判断点D是否在该反比例函数的图象上,并说明理由.
(3)若P(a,b)是反比例函数y=![]() 的图象(x>0)的一点,且S△POC<S△DOC,则a的取值范围为_____.
的图象(x>0)的一点,且S△POC<S△DOC,则a的取值范围为_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,∠AOD=∠COB=90°,∠COE=25°,EO是∠BOD的角平分线;
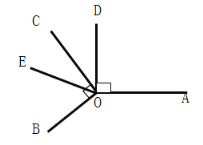
(1)找出图中除直角外的两对相等的角:
(2)求∠COD的度数,按要求填空:
因为∠COB=90°,∠COE=25°,
所以∠BOE=∠ -∠ =90°- °= °.
因为EO是∠BOD的角平分线,
所以∠ =∠BOE= °
所以∠COD=∠ -∠ = °- °= °.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,规定:抛物线y=a(x﹣h)2+k的关联直线为y=a(x﹣h)+k.
例如:抛物线y=2(x+1)2﹣3的关联直线为y=2(x+1)﹣3,即y=2x﹣1.
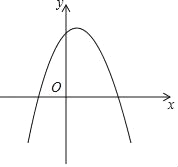
(1)如图,对于抛物线y=﹣(x﹣1)2+3.
①该抛物线的顶点坐标为_____,关联直线为_____,该抛物线与其关联直线的交点坐标为_____和_____;
②点P是抛物线y=﹣(x﹣1)2+3上一点,过点P的直线PQ垂直于x轴,交抛物线y=﹣(x﹣1)2+3的关联直线于点Q.设点P的横坐标为m,线段PQ的长度为d(d>0),求当d随m的增大而减小时,d与m之间的函数关系式,并写出自变量m的取值范围.
(2)顶点在第一象限的抛物线y=﹣a(x﹣1)2+4a与其关联直线交于点A,B(点A在点B的左侧),与x轴负半轴交于点C,直线AB与x轴交于点D,连结AC、BC.
①求△BCD的面积(用含a的代数式表示).
②当△ABC为钝角三角形时,直接写出a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
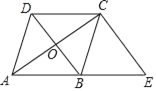
【题目】如图,已知菱形ABCD的对角线AC,BD相交于点O,过C作CE⊥AC,交AB的延长线于点E.
(1)求证:四边形BECD是平行四边形;
(2)若∠E=50°,求∠DAB的度数.
查看答案和解析>>
科目: 来源: 题型:
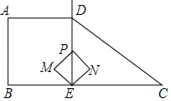
【题目】如图,在四边形ABCD中,AD∥BC,∠B=90°,射线ED⊥BC于点E,AD=AB=BE=![]() BC=4,动点P从点E出发,沿射线ED以每秒2个单位长度的速度运动,以PE为对角线做正方形PMEN,设运动时间为t秒,正方形PMEN与四边形ABCD重叠部分面积为S.
BC=4,动点P从点E出发,沿射线ED以每秒2个单位长度的速度运动,以PE为对角线做正方形PMEN,设运动时间为t秒,正方形PMEN与四边形ABCD重叠部分面积为S.
(1)当点N落在边DC上时,求t的值.
(2)求S与t的函数关系式.
(3)当正方形PMEN被直线BD分成2:1两部分时,直接写出t的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在学校组织的知识竞赛活动中,老师将八年级一班和二班全部学生的成绩整理并绘制成如下统计表:
得分(分) 人数(人) 班级 | 50 | 60 | 70 | 80 | 90 | 100 |
一班 | 2 | 5 | 10 | 13 | 14 | 6 |
二班 | 4 | 4 | 16 | 2 | 12 | 12 |
(1)现已知一班和二班的平均分相同,请求出其平均分.
(2)请分别求出这两班的中位数和众数,并进一步分析这两个班级在这次竞赛中成绩的情况.
查看答案和解析>>
科目: 来源: 题型:
【题目】定义:在三角形中,把一边的中点到这条边的高线的距离叫做这条边的中垂距.
例:如图①,在△ABC中,D为边BC的中点,AE⊥BC于E,则线段DE的长叫做边BC的中垂距.
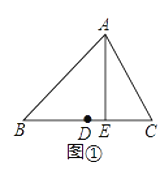
(1)设三角形一边的中垂距为d(d≥0).若d=0,则这样的三角形一定是________,推断的数学依据是________.
(2)如图②,在△ABC中,∠B=45°,AB=![]() ,BC=8,AD为边BC的中线,求边BC的中垂距.
,BC=8,AD为边BC的中线,求边BC的中垂距.

(3)如图③,在矩形ABCD中,AB=6,AD=4.点E为边CD的中点,连结AE并延长交BC的延长线于点F,连结AC.求△ACF中边AF的中垂距.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,A、B两点在数轴上对应的数分别为a,b,且点A在点B的左侧;
![]()
(1)列方程解应用题:若AB的长度为115个单位长度,现有已知蚂蚁P从A出发,以每秒3个单位长度的速度向右运动,5秒之后,另一只蚂蚁Q从点B出发,以每秒2个单位长度的速度向左运动,求蚂蚁Q出发多长时间后,两只蚂蚁在数轴上相遇?
(2)若∣a∣=20,a+b=100,ab<0,请求出a,b的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在结束了380课时初中阶段教学内容的教学后,刘老师计划在增加60课时用于总复习,将380课时按内容所占比例,绘制如下统计图表(图1和~图2),请根据图表提供的信息,回答下列问题:

(1)图1中“统计与概率”所在扇形的圆心角为度;
(2)图2中的a= ;
(3)在60课时的总复习中,刘老师应安排多少课时复习“数与代数”内容?为什么?
查看答案和解析>>
科目: 来源: 题型:
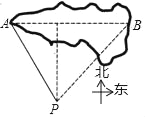
【题目】在数学活动课上,九年级(1)班数学兴趣小组的同学们要测量某公园人工湖亭子A与它正东方向的亭子B之间的距离,现测得亭子A位于点P北偏西30°方向,亭子B位于点P北偏东42°方向,测得点P与亭子A之间的距离为200米,求亭子A与亭子B之间的距离.(结果精确到1米)
【参考数据:sin42°=0.67,cos42°=0.74,tan42°=0.90, ![]() =1.73】
=1.73】
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com