
科目: 来源: 题型:
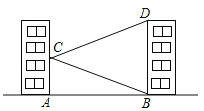
【题目】如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C测得教学楼顶部D的仰角为18°,教学楼底部B的俯角为20°,量得实验楼与教学楼之间的距离AB=30m.
(1)求∠BCD的度数.
(2)求教学楼的高BD.(结果精确到0.1m,参考数据:tan20°≈0.36,tan18°≈0.32)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与x轴,y轴分别交于A,B两点,点
与x轴,y轴分别交于A,B两点,点![]() 为直线
为直线![]() 上一点,直线
上一点,直线![]() 过点C.
过点C.

![]() 求m和b的值;
求m和b的值;
![]() 直线
直线![]() 与x轴交于点D,动点P从点D开始以每秒1个单位的速度向x轴负方向运动
与x轴交于点D,动点P从点D开始以每秒1个单位的速度向x轴负方向运动![]() 设点P的运动时间为t秒.
设点P的运动时间为t秒.
①若点P在线段DA上,且![]() 的面积为10,求t的值;
的面积为10,求t的值;
②是否存在t的值,使![]() 为等腰三角形?若存在,直接写出t的值;若不存在,请说明理由.
为等腰三角形?若存在,直接写出t的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在ABCD中,已知AB=6,BE平分∠ABC交AD边于点E,点E将AD分为1:3两部分,则AD的长为( )
A. 8或24B. 8C. 24D. 9或24
查看答案和解析>>
科目: 来源: 题型:
【题目】正方形ABCD,CEFG按如图放置,点B,C,E在同一条直线上,点P在BC边上,PA=PF,且∠APF=90°,连接AF交CD于点M,有下列结论:①EC=BP;②AP=AM;③∠BAP=∠GFP;④AB2+CE2=![]() AF2;⑤S正方形ABCD+S正方形CEFG=2S△APF.其中正确的是( )
AF2;⑤S正方形ABCD+S正方形CEFG=2S△APF.其中正确的是( )
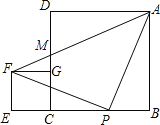
A. ①②③ B. ①③④ C. ①②④⑤ D. ①③④⑤
查看答案和解析>>
科目: 来源: 题型:
【题目】若n是一个两位正整数,且n的个位数字大于十位数字,则称n为“两位递增数”(如13,35,56等).在某次数学趣味活动中,每位参加者需从由数字1,2,3,4,5,6构成的所有的“两位递增数”中随机抽取1个数,且只能抽取一次.
(1)写出所有个位数字是5的“两位递增数”;
(2)请用列表法或树状图,求抽取的“两位递增数”的个位数字与十位数字之积能被10整除的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】在圆O中,C是弦AB上的一点,联结OC并延长,交劣弧AB于点D,联结AO、BO、AD、BD. 已知圆O的半径长为5 ,弦AB的长为8.
(1)如图1,当点D是弧AB的中点时,求CD的长;
(2)如图2,设AC=x, ![]() ,求y关于x的函数解析式并写出定义域;
,求y关于x的函数解析式并写出定义域;
(3)若四边形AOBD是梯形,求AD的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】平面直角坐标系xOy中,已知点A(0,3)、点B(3,0),一次函数y=2x的图象与直线AB交于点M.
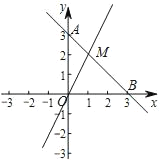
(1)求直线AB的函数解析式及M点的坐标;
(2)若点N是x轴上一点,且△MNB的面积为6,求点N的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】探索与猜想:
有一列数: 第一个数是![]() ,第二个数
,第二个数![]() ,第三个数开始依次记为
,第三个数开始依次记为![]() 、..从第二个数开始,每个数是它相邻两数和的一半.
、..从第二个数开始,每个数是它相邻两数和的一半.
(1)则第三、四、五个数分别为 、 、 ;
(2)推测![]() ______ ;
______ ;
(3)猜想第![]() 个数
个数![]() .
.
(4)计算: ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图在直角坐标平面内,抛物线![]() 与
与![]() 轴交于点A,与x轴分别交于点B(-1,0)、点C(3,0),点D是抛物线的顶点.
轴交于点A,与x轴分别交于点B(-1,0)、点C(3,0),点D是抛物线的顶点.
(1)求抛物线的表达式及顶点D的坐标;
(2)连接AD、DC,求![]() 的面积;
的面积;
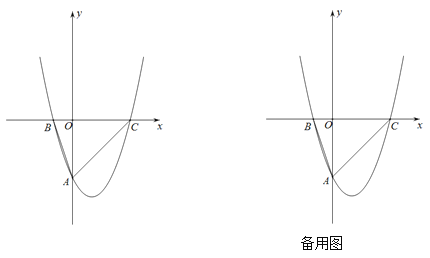
(3)点P在直线DC上,联结OP,若以O、P、C为顶点的三角形与△ABC相似,求点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校要从甲乙两名射击运动员中挑选一人参加全市比赛,在选拔赛中,每人进行了5次射击,甲的成绩(环)为:9.7,10,9.6,9.8,9.9;乙的成绩的平均数为9.8,方差为0.032;
(1)甲的射击成绩的平均数和方差分别是多少?
(2)据估计,如果成绩的平均数达到9.8环就可能夺得金牌,为了夺得金牌,应选谁参加比赛?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com