
科目: 来源: 题型:
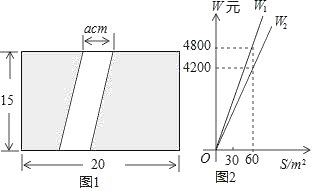
【题目】如图1,为美化校园环境,某校计划在一块长为20m,宽为15m的长方形空地上修建一条宽为a(m)的甬道,余下的部分铺设草坪建成绿地.
(1)甬道的面积为 m2,绿地的面积为 m2(用含a的代数式表示);
(2)已知某公园公司修建甬道,绿地的造价W1(元),W2(元)与修建面积S之间的函数关系如图2所示.①园林公司修建一平方米的甬道,绿地的造价分别为 元, 元.②直接写出修建甬道的造价W1(元),修建绿地的造价W2(元)与a(m)的关系式;③如果学校决定由该公司承建此项目,并要求修建的甬道宽度不少于2m且不超过5m,那么甬道宽为多少时,修建的甬道和绿地的总造价最低,最低总造价为多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,在ABCD中,对角线AC,BD交于点O,AB⊥AC,AB=1,BC=![]() .
.
(1)求平行四边形ABCD的面积S□ABCD;
(2)求对角线BD的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】一般地,任何一个无限循环小数都可以写成分数形式,现以无限循环小数0.![]() 为例进行讨论:设0.
为例进行讨论:设0.![]() =x,由0.
=x,由0.![]() =0.777…可知,10x﹣x=7.
=0.777…可知,10x﹣x=7.![]() ﹣0.
﹣0.![]() =7,即10x﹣x=7.解方程,得x=
=7,即10x﹣x=7.解方程,得x=![]() .于是,得0.
.于是,得0. ![]() =
= ![]() .则0.
.则0.![]() =____________;0.
=____________;0.![]()
![]() =____________ .
=____________ .
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司计划投入50万元,开发并生产甲乙两种产品,根据市场调查预计甲产品的年获利y1(万元)与投入资金x(万元)成正比例,乙产品的年获利y2(万元)与投入资金x(万元)的平方成正比例,设该公司投入乙产品x(万元),两种产品的年总获利为y万元(x≥0),得到了表中的数据.
x(万元) | 20 | 30 |
y(万元) | 10 | 13 |
(1)求y与x的函数关系式;
(2)该公司至少可获得多少利润?请你利用所学的数学知识对该公司投入资金的分配提出合理化建
议,使他能获得最大利润,并求出最大利润是多少?
(3)若从年总利润扣除投入乙产品资金的a倍(a≤1)后,剩余利润随x增大而减小,求a的取值
范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】王先生到泉州台商投资区行政服务中心大楼办事,假定乘电梯向上一楼记作+1,向下一楼记作﹣1,王先生从1楼出发,电梯上下楼层依次记录如下:(单位:层)
+6,﹣3,+10,﹣8,+12,﹣7,﹣10.
(1)请你通过计算说明王先生最后是否回到出发点1楼.
(2)该中心大楼每层高3m,电梯每向上或下1m需要耗电0.1度,根据王先生现在所处位置,请你算算,他办事时电梯需要耗电多少度?
查看答案和解析>>
科目: 来源: 题型:
【题目】某种计时“香篆”在0:00时刻点燃,若“香篆”剩余的长度h(cm)与燃烧的时间x(h)之间是一次函数关系,h与x的一组对应数值如表所示:
燃烧的时间x(h) | … | 3 | 4 | 5 | 6 | … |
剩余的长度h(cm) | … | 210 | 200 | 190 | 180 | … |
(1)写出“香篆”在0:00时刻点然后,其剩余的长度h(cm)与燃烧时间x(h)的函数关系式,并解释函数表达式中x的系数及常数项的实际意义;
(2)通过计算说明当“香篆”剩余的长度为125cm时的时刻.

查看答案和解析>>
科目: 来源: 题型:
【题目】矩形ABCD中,点C(3,8),E、F为AB、CD边上的中点,如图1,点A在原点处,点B在y轴正半轴上,点C在第一象限,若点A从原点出发,沿x轴向右以每秒1个单位长度的速度运动,点B随之沿y轴下滑,并带动矩形ABCD在平面内滑动,如图2,设运动时间表示为t秒,当点B到达原点时停止运动.
(1)当t=0时,点F的坐标为 ;
(2)当t=4时,求OE的长及点B下滑的距离;
(3)求运动过程中,点F到点O的最大距离;
(4)当以点F为圆心,FA为半径的圆与坐标轴相切时,求t的值.

查看答案和解析>>
科目: 来源: 题型:
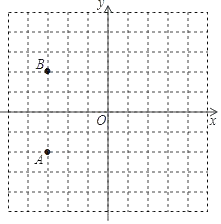
【题目】如图,在直角坐标系中,已知点O,A的坐标分别为(0,0),(﹣3,﹣2).
(1)点B的坐标是 ,点B与点A的位置关系是 .现将点B,点A都向右平移5个单位长度分别得到对应点C和D,顺次连接点A,B,C,D,画出四边形ABCD;
(2)横、纵坐标都是整数的点成为整数点,在四边形ABCD内部(不包括边界)的整数点M使S△ABM=8,请直接写出所有点M的可能坐标;
(3)若一条经过点(0,﹣4)的直线把四边形ABCD的面积等分,则这条直线的表达式是 ,并在图中画出这条直线.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线l的解析式y=kx+3(k<0)与y轴交于A点,
与x轴交于点B.点C的坐标为(4,2).
(1)点A的坐标为 ;
(2)若将△AOB沿直线l折叠,能否使点O与点C重合,若能求此时直线l的解析式;若不能,请说明理由。
(3)若点C在直线l的下方,求k的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图:在数轴上A点表示数a,B点示数b,C点表示数c,b是最小的正整数,且a,b满足![]() +(c-7)2=0.
+(c-7)2=0.
(1) a= ,b= ,c= .
(2) 若将数轴折叠,使得A点与C点重合,则点B与数 表示的点重合.
(3) 点A,B,C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动,假设t秒钟过后,若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.则AB= ,AC= ,BC= .(用含t的代数式表示)
(4) 请问:3BC-2AB的值是否随着时间t的变化而改变? 若变化,请说明理由;若不变,请求其值.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com