根据其中的规律，在数表中的方框内由上到下的数分别是_____、_____．

A. （（k﹣1）n，0） B. （（k+）n，0）） C. （，0） D. （（k+1）n，0）

（1）3+（﹣）﹣（﹣）+2．

（2）（﹣5）×6+（﹣125）÷（﹣5）．

（3）（+）×（﹣48）．

（4）﹣12018×[（﹣2）5﹣32﹣÷（﹣）]﹣2.5．

（1）求该抛物线的解析式；

（2）如图2，过点A作BE的平行线交抛物线于另一点D，点P是抛物线上位于线段AD下方的一个动点，连结PA，EA，ED，PD，求四边形EAPD面积的最大值；

（3）如图3，连结AC，将△AOC绕点O逆时针方向旋转，记旋转中的三角形为△A′OC′，在旋转过程中，直线OC′与直线BE交于点Q，若△BOQ为等腰三角形，请直接写出点Q的坐标．

材料：在学习绝对值时，老师教过我们绝对值的几何含义，如|5﹣3|表示5、3在数轴上对应的两点之间的距离；|5+3|=|5﹣（﹣3）|，所以|5+3|表示5、﹣3在数轴上对应的两点之间的距离；|5|=|5﹣0|，所以|5|表示5在数轴上对应的点到原点的距离．一般地，点A、B在数轴上分别表示有理数a、b，那么A、B之间的距离可表示为|a﹣b|．

问题（1）：点A、B、C在数轴上分别表示有理数﹣5、﹣1、3，那么A到B的距离是　　　　　　，

A到C的距离是　　 　　　. （直接填最后结果）．

问题（2）：点A、B、C在数轴上分别表示有理数x、﹣2、1，那么A到B的距离与A到C的距离之和可表示为　　　 　 　　（用含绝对值的式子表示）．

问题（3）：利用数轴探究：①找出满足|x﹣3|+|x+1|=6的x的所有值是　　 　 　　　；

②设|x﹣3|+|x+1|=p，当x的值取在不小于﹣1且不大于3的范围时，p的值是不变的，而且是p的最小值，这个最小值是　　　　　　；当x的值取在　　　　 　　的范围时，|x|+|x﹣2|的最小值是　　　　　　．

问题（4）：求|x﹣3|+|x﹣2|+|x+1|的最小值以及此时x的值.

【题目】如图，四边形是矩形纸片且，对折矩形纸片，使与重合，折痕为，展平后再过点折叠矩形纸片，使点落在上的点处，折痕与相交于点，再次展开，连接，.

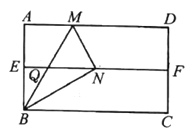
（1）连接，求证：是等边三角形；

（2）求，的长；

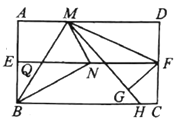
（3）如图，连接将沿折叠，使点落在点处，延长交边于点，已知，求的长？

A家规定：批发数量不超过1000千克，按零售价的92%优惠；批发数量不超过2000千克，按零售价的90%优惠；超过2000千克的按零售价的88%优惠．

B家的规定如下表：

（1）如果他批发700千克苹果，则他在A、B两家批发分别需要多少元？

（2）如果他批发x千克苹果（1500＜x＜2000），请你分别用含x的代数式表示他在A、B两家批发所需的费用；

（3）A、B两店在互相竞争中开始了互怼，B说A店的苹果总价有不合理的，有时候买的少反而贵，忽悠消费者；A说B的总价计算太麻烦，把消费者都弄糊涂了；旁边陆老师听完，提出两个问题希望同学们帮忙解决：

问题1：能否举例说明A店买的多反而便宜?

问题2：B店老板比较聪明，在平时工作中发现有巧妙的方法：总价=购买数量×单价+价格补贴；

注:不同的单价，补贴价格也不同；只需提前算好即可填下表：

（1）当x=﹣2， y=0.6时，求A+2B的值；

（2）若代数式2A﹣B的结果与字母y的取值无关，求x的值

【题目】如图①，Rt△ABC中，∠B=90°，∠CAB=30°，它的顶点A的坐标为（10，0），顶点B的坐标为（5，5），AB=10，点P从点A出发，沿A→B→C的方向匀速运动，同时点Q从点D（0，2）出发，沿y轴正方向以相同速度运动，当点P到达点C时，两点同时停止运动，设运动的时间为t秒．

（1）当点P在AB上运动时，△OPQ的面积S（平方单位）与时间t（秒）之间的函数图象为抛物线的一部分，（如图②），则点P的运动速度为 ；

（2）求（1）中面积S与时间t之间的函数关系式及面积S的最大值及S取最大值时点P的坐标；

（3）如果点P，Q保持（1）中的速度不变，那么点P沿AB边运动时，∠OPQ的大小随着时间t的增大而增大；沿着BC边运动时，∠OPQ的大小随着时间t的增大而减小，当点P沿这两边运动时，使∠OPQ=90°的点P有 个．

①2x2﹣4x+1+2x﹣5x2

②（8x﹣3x2）﹣5xy﹣2（3xy﹣2x2）

（2）先化简，再求值：（3x2y+5x）﹣[x2y﹣4（x﹣x2y）]，其中（x+2）2+|y﹣3|=0