
科目: 来源: 题型:
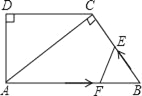
【题目】如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5).
(1)求证:△ACD∽△BAC;
(2)求DC的长;
(3)设四边形AFEC的面积为y,求y关于t的函数关系式,并求出y的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知O是AB上的一点,从O点引出射线OC、OE、OD,其中OE平分∠BOC.
(1)如图1,若∠COD是直角,∠DOE=15°,求∠AOE的度数;
(2)如图1,若∠AOC=∠BOD,∠DOE=15°,求∠AOE的度数;
(3)将图1中的∠COD (∠COD仍是直角)绕顶点O顺时针旋转至图2的位置,若∠AOC=![]() , ∠DOE=
, ∠DOE=![]() ,请猜想
,请猜想![]() 与
与![]() 之间存在什么样的数量关系,写出你的结论,并说明理由.
之间存在什么样的数量关系,写出你的结论,并说明理由.

查看答案和解析>>
科目: 来源: 题型:
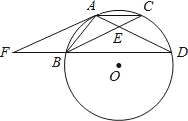
【题目】如图,点A,B,C,D在⊙O上,AB=AC,AD与BC相交于点E,AE=![]() ED,延长DB到点F,使FB=
ED,延长DB到点F,使FB=![]() BD,连接AF.
BD,连接AF.
(1)证明:△BDE∽△FDA;
(2)试判断直线AF与⊙O的位置关系,并给出证明.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图矩形ABCD中,AB=12,BC=8,E、F分别为AB、CD的中点,点P、Q从A. C同时出发,在边AD、CB上以每秒1个单位向D、B运动,运动时间为t(0<t<8).
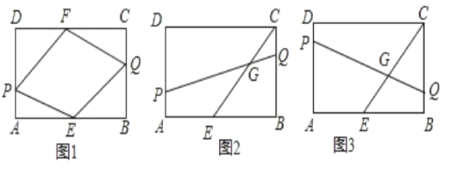
(1)如图1,连接PE、EQ、QF、PF,求证:无论t在0<t<8内取任何值,四边形PEQF总为平行四边形;
(2)如图2,连接PQ交CE于G,若PG=4QG,求t的值;
(3)在运动过程中,是否存在某时刻使得PQ⊥CE于G?若存在,请求出t的值:若不存在,请说明理由
查看答案和解析>>
科目: 来源: 题型:
【题目】一个几何体是由若干个棱长为3cm的小正方体搭成的,从左面、上面看到的几何体的形状图如图所示:
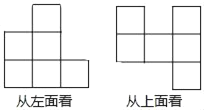
(1)该几何体最少由 个小立方体组成,最多由 个小立方体组成.
(2)将该几何体的形状固定好,
①求该几何体体积的最大值;
②若要给体积最小时的几何体表面涂上油漆,求所涂油漆面积的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知如图,在数轴上有A,B两点,所表示的数分别为-10,4,点A以每秒5个单位长度的速度向右运动,同时点B以每秒3个单位长度的速度也向左运动,如果设运动时间为t秒,解答下列问题:![]()
(1)运动前线段AB的长为 ; 运动1秒后线段AB的长为 ;
(2)运动t秒后,点A,点B运动的距离分别为 ;用t表示A,B分别为 .
(3)求t为何值时,点A与点B恰好重合;
(4)在上述运动的过程中,是否存在某一时刻t,使得线段AB的长为6,若存在,求t的值; 若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知一次函数y=![]() x3与反比例函数y=
x3与反比例函数y=![]() 的图象相交于点A(4,n),与x轴相交于点B.
的图象相交于点A(4,n),与x轴相交于点B.

(1)填空:n的值为___,k的值为___;
(2)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标;
(3)观察反比例函数y=![]() 的图象,当y2时,请直接写出自变量x的取值范围。
的图象,当y2时,请直接写出自变量x的取值范围。
查看答案和解析>>
科目: 来源: 题型:
【题目】某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回),商场根据两小球所标金额的和返还相应价格购物券,可以重新在本商场消费,某顾客刚好消费200元.
(1)该顾客至少可得到_____元购物券,至多可得到_______元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.
查看答案和解析>>
科目: 来源: 题型:
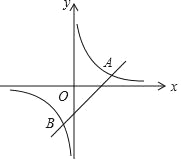
【题目】如图,已知一次函数y=x﹣2与反比例函数y=![]() 的图象交于A、B两点.
的图象交于A、B两点.
(1)求A、B两点的坐标;
(2)观察图象,直接写出一次函数值小于反比例函数值的x的取值范围;
(3)坐标原点为O,求△AOB的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,过点A作AD⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G.F为AB边上一点,连接CF,且∠ACF=∠CBG.
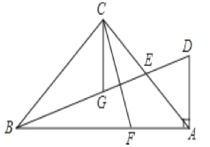
(1)求证:BG=CF;
(2)求证:CF=2DE;
(3)若DE=1,求AD的长
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com