
科目: 来源: 题型:
【题目】如图,已知四点A、B、C、D.
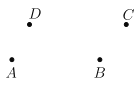
(1)用圆规和无刻度的直尺按下列要求与步骤画出图形:
①画直线AB.
②画射线DC.
③延长线段DA至点E,使![]() .(保留作图痕迹)
.(保留作图痕迹)
④画一点P,使点P既在直线AB上,又在线段CE上.
(2)在(1)中所画图形中,若![]() cm,
cm,![]() cm,点F为线段DE的中点,求AF的长.
cm,点F为线段DE的中点,求AF的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知,抛物线y=ax2+ax+b(a≠0)与直线y=2x+m有一个公共点M(1,0),且a<b.
(1)求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示);
(2)直线与抛物线的另外一个交点记为N,求△DMN的面积与a的关系式;
(3)a=﹣1时,直线y=﹣2x与抛物线在第二象限交于点G,点G、H关于原点对称,现将线段GH沿y轴向上平移t个单位(t>0),若线段GH与抛物线有两个不同的公共点,试求t的取值范围.

【答案】(1)b=﹣2a,顶点D的坐标为(﹣![]() ,﹣
,﹣![]() );(2)
);(2)![]() ;(3) 2≤t<
;(3) 2≤t<![]() .
.
【解析】试题分析:(1)把M点坐标代入抛物线解析式可得到b与a的关系,可用a表示出抛物线解析式,化为顶点式可求得其顶点D的坐标;
(2)把点![]() 代入直线解析式可先求得m的值,联立直线与抛物线解析式,消去y,可得到关于x的一元二次方程,可求得另一交点N的坐标,根据a<b,判断a<0,确定D、M、N的位置,画图1,根据面积和可得
代入直线解析式可先求得m的值,联立直线与抛物线解析式,消去y,可得到关于x的一元二次方程,可求得另一交点N的坐标,根据a<b,判断a<0,确定D、M、N的位置,画图1,根据面积和可得![]() 的面积即可;
的面积即可;
(3)先根据a的值确定抛物线的解析式,画出图2,先联立方程组可求得当GH与抛物线只有一个公共点时,t的值,再确定当线段一个端点在抛物线上时,t的值,可得:线段GH与抛物线有两个不同的公共点时t的取值范围.
试题解析:(1)∵抛物线![]() 有一个公共点M(1,0),
有一个公共点M(1,0),
∴a+a+b=0,即b=2a,
![]()
∴抛物线顶点D的坐标为![]()
(2)∵直线y=2x+m经过点M(1,0),
∴0=2×1+m,解得m=2,
∴y=2x2,
则![]()
得![]()
∴(x1)(ax+2a2)=0,
解得x=1或![]()
∴N点坐标为![]()
∵a<b,即a<2a,
∴a<0,
如图1,设抛物线对称轴交直线于点E,

∵抛物线对称轴为![]()
![]()
![]()
设△DMN的面积为S,
![]()
(3)当a=1时,
抛物线的解析式为:![]()
有![]()
![]()
解得:![]()
∴G(1,2),
∵点G、H关于原点对称,
∴H(1,2),
设直线GH平移后的解析式为:y=2x+t,
x2x+2=2x+t,
x2x2+t=0,
△=14(t2)=0,
![]() 当点H平移后落在抛物线上时,坐标为(1,0),
当点H平移后落在抛物线上时,坐标为(1,0),
把(1,0)代入y=2x+t,
t=2,
∴当线段GH与抛物线有两个不同的公共点,t的取值范围是![]()

【题型】解答题
【结束】
24
【题目】在△ABC中,AB=AC,点D是直线BC上的一点(不与B,C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE,设∠BAC=α,∠BCE=β.
(1)如图①,当点D在线段BC上,如果α=60°,β=120°;
如图②,当点D在线段BC上,如果α=90°,β=90°
如图③,当点D在线段BC上,如果α,β之间有什么样的关系?请直接写出.
(2)如图④,当点D在射线BC上,(1)中结论是否成立?请说明理由.
(3)如图⑤,当点D在射线CB上,且在线段BC外,(1)中结论是否成立?若不成立,请直接写出你认为正确的结论.

查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两座城市的中心火车站A,B两站相距360 km.一列动车与一列特快列车分别从A,B两站同时出发相向而行,动车的平均速度比特快列车快54 km/h,当动车到达B站时,特快列车恰好到达距离A站135 km处的C站.求动车和特快列车的平均速度各是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过点O作OE∥AB,交BC于E.
(1)求证:ED为⊙O的切线;
(2)如果⊙O的半径为![]() ,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.
,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.

【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)首先连接OD,由OE∥AB,根据平行线与等腰三角形的性质,易证得![]() ≌
≌![]() 即可得
即可得![]() ,则可证得
,则可证得![]() 为
为![]() 的切线;
的切线;
(2)连接CD,根据直径所对的圆周角是直角,即可得![]() 利用勾股定理即可求得
利用勾股定理即可求得![]() 的长,又由OE∥AB,证得
的长,又由OE∥AB,证得![]() 根据相似三角形的对应边成比例,即可求得
根据相似三角形的对应边成比例,即可求得![]() 的长,然后利用三角函数的知识,求得
的长,然后利用三角函数的知识,求得![]() 与
与![]() 的长,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.
的长,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.
试题解析:(1)证明:连接OD,

∵OE∥AB,
∴∠COE=∠CAD,∠EOD=∠ODA,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠COE=∠DOE,
在△COE和△DOE中,
 ∴△COE≌△DOE(SAS),
∴△COE≌△DOE(SAS),
![]()
∴ED⊥OD,
∴ED是![]() 的切线;
的切线;
(2)连接CD,交OE于M,
在Rt△ODE中,
∵OD=32,DE=2,
![]()
∵OE∥AB,
∴△COE∽△CAB,
![]() ∴AB=5,
∴AB=5,
∵AC是直径,
![]()
![]()
![]()
![]()
∵EF∥AB,
![]()
![]()
![]()
∴S△ADF=S梯形ABEFS梯形DBEF
![]()
∴△ADF的面积为![]()

【题型】解答题
【结束】
25
【题目】【题目】已知,抛物线y=ax2+ax+b(a≠0)与直线y=2x+m有一个公共点M(1,0),且a<b.
(1)求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示);
(2)直线与抛物线的另外一个交点记为N,求△DMN的面积与a的关系式;
(3)a=﹣1时,直线y=﹣2x与抛物线在第二象限交于点G,点G、H关于原点对称,现将线段GH沿y轴向上平移t个单位(t>0),若线段GH与抛物线有两个不同的公共点,试求t的取值范围.

查看答案和解析>>
科目: 来源: 题型:
【题目】在数轴上,点A,O,B分别表示﹣15,0,9,点P,Q分别从点A,B同时开始沿数轴正方向运动,点P的速度是每秒3个单位,点Q的速度是每秒1个单位,运动时间为t秒.在运动过程中,若点P,Q,O三点其中一个点恰好是另外两点为端点的线段的一个三等分点,则运动时间为_____秒.
查看答案和解析>>
科目: 来源: 题型:
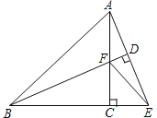
【题目】如图,在△ABC中,AC⊥BC,AC=BC,延长BC至E使BE=BA,过点B作BD⊥AE于点D,BD与AC交于点F,连接EF.
(1)求证:△ACE≌△BCF.
(2)求证:BF=2AD,
(3)若CE=![]() ,求AC的长.
,求AC的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某工程队承包了某段全长1800米的过江隧道施工任务,甲、乙两个班组分别从东、西两端同时掘进,已知甲组比乙组平均每天多掘进2米,经过5天施工,两组共掘进了60米,为加快工程进度,通过改进施工技术,在剩余的工程中,甲组平均每天能比原来多掘进2米,乙组平均每天能比原来多掘进1米,按此施工进度,能够比原来少用______天完成任务.
查看答案和解析>>
科目: 来源: 题型:
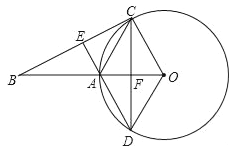
【题目】如图,⊙O的半径为6cm,经过⊙O上一点C作⊙O的切线交半径OA的延长于点B,作∠ACO的平分线交⊙O于点D,交OA于点F,延长DA交BC于点E.
(1)求证:AC∥OD;
(2)如果DE⊥BC,求弧AC的长度.
查看答案和解析>>
科目: 来源: 题型:
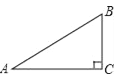
【题目】某校计划把一块近似于直角三角形的废地开发为生物园,如图所示,∠ACB=90°,BC=60米,∠A=36°.
(1)若入口处E在AB边上,且与A、B等距离,求CE的长(精确到个位);
(2)若D点在AB边上,计划沿线段CD修一条水渠.已知水渠的造价为50元/米,水渠路线应如何设计才能使造价最低,求出最低造价.
(其中sin36°=0.5878,cos36°=0.8090,tan36°=0.7265)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com