
科目: 来源: 题型:
【题目】国家环保局统一规定,空气质量分为5级:当空气污染指数达0—50时为1级,质量为优;51—100时为2级,质量为良;101—200时为3级,轻度污染;201—300时为4级,中度污染;300以上时为5级,重度污染.某城市随机抽取了2015年某些天的空气质量检测结果,并整理绘制成如下两幅不完整的统计图.请根据图中信息,解答下列各题:
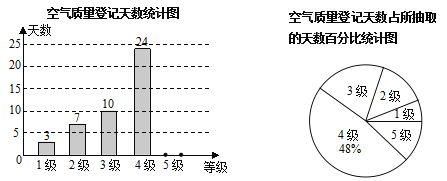
(1) 本次调查共抽取了 天的空气质量检测结果进行统计;
(2) 补全条形统计图;
(3) 扇形统计图中3级空气质量所对应的圆心角为 °;
(4) 如果空气污染达到中度污染或者以上,将不适宜进行户外活动,根据目前的统计,请你估计2015年该城市有多少天不适宜开展户外活动.(2015年共365天)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知如图,边长为2的正方形![]() 中,
中,![]() 是对角线
是对角线![]() 上的一个动点(与点
上的一个动点(与点![]() 、
、![]() 不重合),过点
不重合),过点![]() 作
作![]() ,
,![]() 交射线
交射线![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() .
.
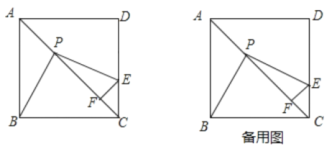
(1)求证:![]() :
:
(2)在点![]() 的运动过程中,
的运动过程中,![]() 的长度是否发生变化?若不变,试求出这个不变的值,写出解答过程:若变化,试说明理由:
的长度是否发生变化?若不变,试求出这个不变的值,写出解答过程:若变化,试说明理由:
(3)在点![]() 的运动过程中,
的运动过程中,![]() 能否为等腰三角形?如果能,直接写出此时
能否为等腰三角形?如果能,直接写出此时![]() 的长;如果不能,试说明理由.
的长;如果不能,试说明理由.
查看答案和解析>>
科目: 来源: 题型:
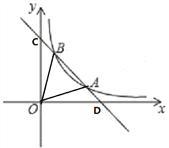
【题目】如图,一次函数y1=﹣2x+8的图象与反比例函数y2=![]() (x>0)的图象交于A(3,n),B(m,6)两点.
(x>0)的图象交于A(3,n),B(m,6)两点.
(1)求反比例函数的解析式;
(2)求△OAB的面积;
(3)根据图象直接写出当x>0时,y1>y2的自变量x的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读材料,解答问题:如果一个四位自然数,十位数字是千位数字的2倍与百位数字的差,个位数字是千位数字的2倍与百位数字的和,则我们称这个四位数“依赖数”,例如,自然数2135,其中3=2×2﹣1,5=2×2+1,所以2135是“依赖数”.
(1)请直接写出最小的四位依赖数;
(2)若四位依赖数的后三位表示的数减去百位数字的3倍得到的结果除以7余3,这样的数叫做“特色数”,求所有特色数.
(3)已知一个大于1的正整数m可以分解成m=pq+n4的形式(p≤q,n≤b,p,q,n均为正整数),在m的所有表示结果中,当nq﹣np取得最小时,称“m=pq+n4”是m的“最小分解”,此时规定:F(m)=![]() ,例:20=1×4+24=2×2+24=1×19+14,因为1×19﹣1×1>2×4﹣2×1>2×2﹣2×2,所以F(20)=
,例:20=1×4+24=2×2+24=1×19+14,因为1×19﹣1×1>2×4﹣2×1>2×2﹣2×2,所以F(20)=![]() =1,求所有“特色数”的F(m)的最大值.
=1,求所有“特色数”的F(m)的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】根据某市个人住房房产税征收管理细则,高档住房建筑面积交易单价达到上一年主城区商品住房面积均价的2倍开始征收房产税,2倍(含2倍)到3倍的住房,房产税年税率为0.5%;3倍(含3倍)至4倍的,房产税税率为1%;4倍(含4倍)以上房产税税率为1.2%.细则规定,买房后第二年开始交房产税.相关数据如下表:
征税年份 | 上一年主城区商品房成交建筑面积均价 |
2016年 | 2015年均价6600元/m2 |
2017年 | 2016年均价7000元m2 |
2018年 | 2017年均价7800元m2 |
个人住房房产税应纳税额的计算公式:年应纳税额=建筑面积×建筑面积交易单价×年税率(例如:2015年建筑面积成交单价为20000元/m2的一套100m2商品房,2016年开始第一次交房产税,因6600×3<20000<6600×4,故2016年应交房产税100×20000×1%=20000元,因7000×2<20000<7000×3,故2017年应交房产税=100×20000×0.5%=10000元)
(1)老朱2016年买了一套建筑面积为150m2的大平层户型,2017年交了12000元的房产税,请问老朱买的房子的建筑面积成交单价是多少元/m2?
(2)2017年老张买了和老朱同户型的一套房,建筑面积单价有所上涨,老张通过计算发现,他2017年购房房款与2018年需缴纳的房产税之和比老朱2016年购房房款与2017、2018两年需缴纳的房产税之和多花了121.2万元,问2017年老张买房时建筑面积单价是多少元/m2?
查看答案和解析>>
科目: 来源: 题型:
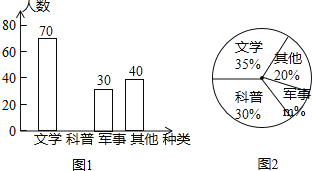
【题目】某学校在开展“书香校园”活动期间,对学生课外阅读的喜好进行抽样调查(每人只选一种书籍),将调查结果绘制成如图所示的两幅不完整的统计图,根据图中的信息,解答下列问题:
(1)这次调查的学生人数为 人,扇形统计图中m的值为 ;
(2)补全条形统计图;
(3)如果这所学校要添置学生课外阅读的书籍1500册,请你估计“科普”类书籍应添置多少册比较合适?
查看答案和解析>>
科目: 来源: 题型:
【题目】某校举办了一次成语知识竞赛,满分10分,学生得分均为整数,成绩达到6分及6分以上为合格,达到9分或10分为优秀. 为了解本次大赛的成绩,校团委随机抽取了甲、乙两组学生成绩作为样本进行统计,绘制了如下统计图表:
组别 | 平均数 | 中位数 | 方差 | 合格率 | 优秀率 |
甲组 | 6.8 | a | 3.76 | 90% | 30% |
乙组 | b | 7.5 | 1.96 | 80% | 20% |
(1)求出表中a,b的值;
(2)小英同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上面的表格判断,小英属于哪个组?
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组. 但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你写出两条支持乙组同学观点的理由.
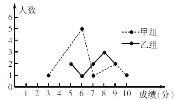
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,已知A、O、B三点在同一直线上,射线OD、OE分别平分∠AOC、∠BOC
(1)求∠DOE的度数;
(2)如图2,在∠AOD内引一条射线OF,使∠COF=![]() ,其他不变,设∠DOF=
,其他不变,设∠DOF=![]()
![]() )
)
①求∠AOF的度数(用含![]() 的代数式表示).
的代数式表示).
②若∠BOD是∠AOF的2倍,求∠DOF的度数.
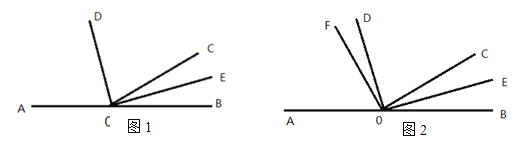
查看答案和解析>>
科目: 来源: 题型:
【题目】网瘾低龄化问题已经引起社会各界的高度关注,有关部门在全国范围内对12﹣35岁的网瘾人群进行了简单的随机抽样调查,绘制出以下两幅统计图.
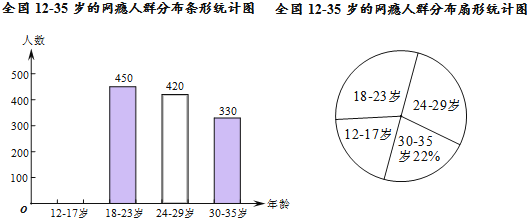
请根据图中的信息,回答下列问题:
(1)这次抽样调查中共调查了 人,并请补全条形统计图;
(2)扇形统计图中18﹣23岁部分的圆心角的度数是 度;
(3)据报道,目前我国12﹣35岁“网瘾人数”约为2000万,请估计其中12﹣17岁的人数.
查看答案和解析>>
科目: 来源: 题型:
【题目】“五一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游。
 [来
[来
根据以上信息,解答下列问题:
(1)设租车时间为![]() 小时,租用甲公司的车所需费用为
小时,租用甲公司的车所需费用为![]() 元,租用乙公司的车所需费用为
元,租用乙公司的车所需费用为![]() 元,分别求出
元,分别求出![]() ,
,![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)请你帮助小明计算并选择哪个出游方案合算。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com