
科目: 来源: 题型:
【题目】阅读下列材料:
关于x的方程:![]() 的解是
的解是![]() ,
,![]() ;
;![]() 即
即![]() 的解是
的解是![]() ;
;![]() 的解是
的解是![]() ,
,![]() ;
;![]() 的解是
的解是![]() ,
,![]() ;
;![]()
![]() 请观察上述方程与解的特征,比较关于x的方程
请观察上述方程与解的特征,比较关于x的方程![]() 与它们的关系,猜想它的解是什么?并利用“方程的解”的概念进行验证.
与它们的关系,猜想它的解是什么?并利用“方程的解”的概念进行验证.
![]() 由上述的观察、比较、猜想、验证,可以得出结论:
由上述的观察、比较、猜想、验证,可以得出结论:
如果方程的左边是未知数与其倒数的倍数的和,方程的右边的形式与左边完全相同,只是把其中的未知数换成了某个常数,那么这样的方程可以直接得解,请用这个结论解关于x的方程:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】一只箱子里共有3个球,其中2个白球,1个红球,它们除颜色外均相同。
(1)从箱子中任意摸出一个球是白球的概率是多少?
(2)从箱子中任意摸出一个球,不将它放回箱子,搅匀后再摸出一个球,求两次摸出球的都是白球的概率,并画出树状图。
查看答案和解析>>
科目: 来源: 题型:
【题目】关于x的方程2(x﹣3)﹣m=2的解和方程3x﹣7=2x的解相同.
(1)求m的值;
(2)已知线段AB=m,在直线AB上取一点P,恰好使AP=2PB,点Q为PB的中点,求线段AQ的长.
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在平面直角坐标系xoy中,点M在x轴的正半轴上,⊙M交x轴于A、B两点,交y轴于C、D两点,且C为弧AE的中点,AE交y轴于G点,若点A的坐标为(-1,0),AE=4
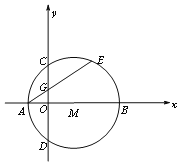
(1)求点C的坐标;
(2)连接MG、BC,求证:MG∥BC
查看答案和解析>>
科目: 来源: 题型:
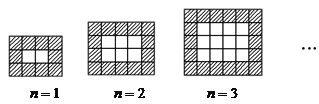
【题目】如图,用同样规格的黑白两色正方形瓷砖铺设长方形地面.请观察各图形并解答有关问题:
(1)在第![]() 个图形中,每一横行共有 块瓷砖,每一竖列共有 块瓷砖(均用含
个图形中,每一横行共有 块瓷砖,每一竖列共有 块瓷砖(均用含![]() 的代数式表示);
的代数式表示);
(2)设铺设地面所用瓷砖的总块数为![]() ,用(1)中的
,用(1)中的![]() 表示
表示![]() ;
;
(3)当![]() =20时,求
=20时,求![]() 的值;
的值;
(4)若黑瓷砖每块4元,白瓷砖每块3元,在问题(3)中,共需花多少元购买瓷砖?
查看答案和解析>>
科目: 来源: 题型:
【题目】有20筐白菜,以每筐30千克为标准,超过或不足的分别用正、负来表示,记录如下:
与标准质量的差(单位:千克) | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
筐数 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)20筐白菜中,最重的一筐比最轻的一筐要重多少千克?
(2)与标准质量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价2元,则出售这20筐白菜可卖多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数y=ax2﹣4ax+3a.
(Ⅰ)求该二次函数的对称轴;
(Ⅱ)若该二次函数的图象开口向下,当1≤x≤4时,y的最大值是2,且当1≤x≤4时,函数图象的最高点为点P,最低点为点Q,求△OPQ的面积;
(Ⅲ)若对于该抛物线上的两点P(x1,y1),Q(x2,y2),当t≤x1≤t+1,x2≥5时,均满足y1≥y2,请结合图象,直接写出t的最大值.
查看答案和解析>>
科目: 来源: 题型:
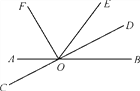
【题目】如图,直线AB与CD相交于点O,OF,OD分别是∠AOE,∠BOE的平分线.
(1)写出∠DOE的补角;
(2)若∠BOE=62°,求∠AOD和∠EOF的度数;
(3)试问射线OD与OF之间有什么特殊的位置关系?为什么?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的两边OA、OC分别在x轴、y轴的正半轴上,OA=4,OC=2.点P从点O出发,沿x轴以每秒1个单位长的速度向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.将线段CP的中点绕点P按顺时针方向旋转90°得点D,点D随点P的运动而运动,连接DP、DA.
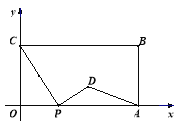
(1)请用含t的代数式表示出点D的坐标;
(2)求t为何值时,△DPA的面积最大,最大为多少?
(3)在点P从O向A运动的过程中,△DPA能否成为直角三角形?若能,求t的值.
若不能,请说明理由;
(4)请直接写出随着点P的运动,点D运动路线的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com