练习册

  • 练习册
  • 试题
    相关习题
     0  355278  355286  355292  355296  355302  355304  355308  355314  355316  355322  355328  355332  355334  355338  355344  355346  355352  355356  355358  355362  355364  355368  355370  355372  355373  355374  355376  355377  355378  355380  355382  355386  355388  355392  355394  355398  355404  355406  355412  355416  355418  355422  355428  355434  355436  355442  355446  355448  355454  355458  355464  355472  366461 

    科目： 来源： 题型：

    【题目】如图，已知△ABC和△ADE都是等腰直角三角形，∠ACB=∠ADE=90°，点F为BE的中点，连接CF，DF．

    （1）如图1，当点D在AB上，点E在AC上时

    ①证明：△BFC是等腰三角形；

    ②请判断线段CF，DF的关系？并说明理由；

    （2）如图2，将图1中的△ADE绕点A旋转到图2位置时，请判断（1）中②的结论是否仍然成立？并证明你的判断．

    查看答案和解析>>

    科目： 来源： 题型：

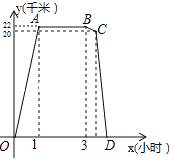
    【题目】某周日上午8：00小宇从家出发，乘车1小时到达某活动中心参加实践活动．11：00时他在活动中心接到爸爸的电话，因急事要求他在12：00前回到家，他即刻按照来活动中心时的路线，以5千米/小时的平均速度快步返回．同时，爸爸从家沿同一路线开车接他，在距家20千米处接上了小宇，立即保持原来的车速原路返回．设小宇离家x（小时）后，到达离家y（千米）的地方，图中折线OABCD表示y与x之间的函数关系．

    （1）活动中心与小宇家相距 千米，小宇在活动中心活动时间为 小时，他从活动中心返家时，步行用了 小时；

    （2）求线段BC所表示的y（千米）与x（小时）之间的函数关系式（不必写出x所表示的范围）；

    （3）根据上述情况（不考虑其他因素），请判断小宇是否能在12：00前回到家，并说明理由．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】有20箱橘子，以每箱25kg为标准，超过或不足的千克数分别用正，负数来表示:记录如下:

    与标准质量的差值（kg）

    -3

    -2

    -1.5

    0

    1

    2.5

    箱数

    1

    4

    2

    3

    2

    8

    （1）与标准重量比较，这20箱橘子总计超过或不足多少千克?

    （2）若橘子每千克售价2.5元，则出售这20箱橘子可卖多少元?

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】20筐白菜，以每筐25千克为标准，超过或不足的千克数分别用正、负数来表示，记录如下：

    与标准偏差

    －3

    －2

    －1.5

    0

    1

    2.5

    筐数

    1

    4

    2

    3

    2

    8

    (1)20筐白菜中，最重的一筐与最轻的一筐相差多少千克？

    (2)这20筐白菜的平均质量比标准质量多或少多少千克？

    (3)若白菜每千克售价2元，则出售这20筐白菜可卖多少元？

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】某科技有限公司准备购进A和B两种机器人来搬运化工材料，已知购进A种机器人2个和B种机器人3个共需16万元，购进A种机器人3个和B种机器人2个共需14万元，请解答下列问题：

    （1）求A、B两种机器人每个的进价；

    （2）已知该公司购买B种机器人的个数比购买A种机器人的个数的2倍多4个，如果需要购买A、B两种机器人的总个数不少于28个，且该公司购买的A、B两种机器人的总费用不超过106万元，那么该公司有哪几种购买方案？

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】如图，已知A（3，m），B（﹣2，﹣3）是直线AB和某反比例函数的图象的两个交点．

    （1）求直线AB和反比例函数的解析式；

    （2）观察图象，直接写出当x满足什么范围时，直线AB在双曲线的下方；

    （3）反比例函数的图象上是否存在点C，使得△OBC的面积等于△OAB的面积？如果不存在，说明理由；如果存在，求出满足条件的所有点C的坐标．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】某公司购买了办公用的A、B两种型号护眼台灯共60盏，花费了 5160元．已知A型台灯每盏80元，B型台灯每盏100元．则A、B两种型号的护 眼台灯各买了多少盏？

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】如图，在△ABC中，∠BAC=90°，AD是中线，E是AD的中点，过点A作AF∥BC交BE的延长线于F，连接CF．

    （1）求证：AD=AF；

    （2）如果AB=AC，试判断四边形ADCF的形状，并证明你的结论．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】如图，在等腰Rt△ABC中，∠ACB＝90°，AC＝CB，F是AB边上的中点，点D、E分别在AC、BC边上运动，且始终保持AD＝CE．连接DE、DF、EF．

    （1）求证：△ADF≌△CEF；

    （2）试证明△DFE是等腰直角三角形．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】如图，直线y=kx-3与x轴、y轴分别相交于B、C两点，且OC=2OB

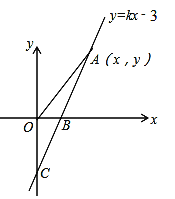
    （1）求B点的坐标和k的值.

    （2）若点A（x,y）是直线y=kx-3上在第一象限内的一个动点，当A 在运动的过程中，试写出△AOB的面积S与x的函数关系式，（不要求写出自变量的取值范围）.

    （3）探究：在（2）的条件下

    ①当A运动到什么位置时，△ABO的面积为，并说明理由.

    ②在①成立的情况下，x轴上是否存在一点P，使△AOP是等腰三角形？若存在，请直接写出满足条件的所有P点的坐标，若不存在，请说明理由.

    查看答案和解析>>

    同步练习册答案