
科目: 来源: 题型:
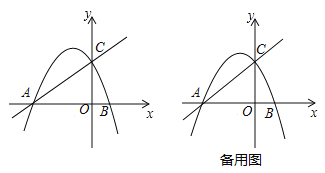
【题目】在直角坐标平面内,直线y=![]() x+2分别与x轴、y轴交于点A、C.抛物线y=﹣
x+2分别与x轴、y轴交于点A、C.抛物线y=﹣![]() +bx+c经过点A与点C,且与x轴的另一个交点为点B.点D在该抛物线上,且位于直线AC的上方.
+bx+c经过点A与点C,且与x轴的另一个交点为点B.点D在该抛物线上,且位于直线AC的上方.
(1)求上述抛物线的表达式;
(2)联结BC、BD,且BD交AC于点E,如果△ABE的面积与△ABC的面积之比为4:5,求∠DBA的余切值;
(3)过点D作DF⊥AC,垂足为点F,联结CD.若△CFD与△AOC相似,求点D的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】某演唱会购买门票的方式有两种.
方式一:若单位赞助广告费10万元,则该单位所购门票的价格为每张0.02万元;
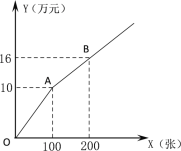
方式二:如图所示.
设购买门票x张,总费用为y万元,方式一中:总费用=广告赞助费+门票费.
(1)求方式一中y与x的函数关系式.
(2)若甲、乙两个单位分别采用方式一、方式二购买本场演唱会门票共400张,且乙单位购买超过100张,两单位共花费27.2万元,求甲、乙两单位各购买门票多少张?
查看答案和解析>>
科目: 来源: 题型:
【题目】按要求完成下列视图问题:
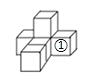
(1)如图(1),它是由6个同样大小的正方体摆成的几何体,将正方体①移走后,新几何体从三个方向看到的图形与原几何体从三个方向看到的图形相比,从 方向看到的形状图没有发生改变?
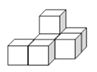
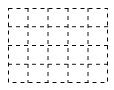
(2)如图(2),请你在右侧虚线网格图a中画出该几何体从上面看到的形状图
(3)如图(3),它是由几个小立方块组成从上面看到的形状图,小正方形上的数字表示该位置上的正方体的个数,请你在右侧建线网格图b中面出该几何体从正面看到的形状图.
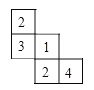
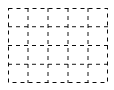
查看答案和解析>>
科目: 来源: 题型:
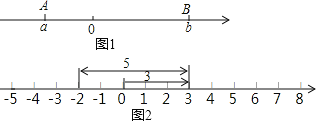
【题目】阅读材料:如图1所示,点A、B在数轴上分别表示有理数a,b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|.例如:|5﹣(﹣2)|表示5与﹣2之差的绝对值,实际上也可理解为5与﹣2两数在数轴上所对应的两点之间的距离.
(1)如图2所示,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动5个单位长度,可以看到终点表示的数是﹣2,利用数形结合思想,请参照下图并思考,完成下列各题:
①数轴上表示2与﹣5的两点之间的距离是 个单位长度.
②若数轴上的点A表示的数为x,点B表示的数为﹣1,则A与B两点的距离可以表示为 ;若|x+1|=3,则x为 .
③如果点A表示数﹣1,将A点向右移动18个单位长度,再向左移动13个单位长度终点为B,那么A,B两点间的距离是 .
(2)若数轴上的点A表示的数为x且x为整数,则当x为 时,|x+5|与|x﹣7|的值相等.
查看答案和解析>>
科目: 来源: 题型:
【题目】在有些情况下,不需要计算出结果也能把绝对值符号去掉。例如:|6+7|= 6+7 ;|6—7|=7- 6;|7-6|=7- 6 ;|―6―7|=6+7;根据上面的规律,把下列各式写成去掉绝对值符号的形式:
(1)|7-21|=______;
(2)|![]() |=_______;
|=_______;
(3)|![]() |=________;
|=________;
(4)用合理的方法计算:|![]() |+|
|+|![]() |-|
|-|![]() |.
|.
查看答案和解析>>
科目: 来源: 题型:
【题目】某电信检修小组从A地出发,在东西向的公路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下.(单位:km)

(1)求收工时距A地多远?
(2)在第几次纪录时距A地最远?
(3)若每km耗油0.2升,问共耗油多少升?
查看答案和解析>>
科目: 来源: 题型:
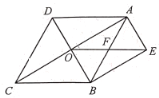
【题目】如图,菱形ABCD的对角线AC、BD相交于点O,BE∥AC,AE∥BD,OE与AB交于点F.
(1)试判断四边形AEBO的形状,并说明理由;
(2)若OE=10,AC=16,求菱形ABCD的面积.
查看答案和解析>>
科目: 来源: 题型:
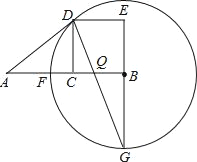
【题目】设C为线段AB的中点,四边形BCDE是以BC为一边的正方形.以B为圆心,BD长为半径的⊙B与AB相交于F点,延长EB交⊙B于G点,连接DG交于AB于Q点,连接AD.
求证:(1)AD是⊙B的切线;(2)AD=AQ;(3)BC2=CFEG.
查看答案和解析>>
科目: 来源: 题型:
【题目】为积极响应“弘扬传统文化”的号召,某学校倡导全校1200名学生进行经典诗词诵背活动,并在活动之后举办经典诗词大赛,为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取部分学生调查“一周诗词诵背数量”,根调查结果绘制成的统计图(部分)如图所示.
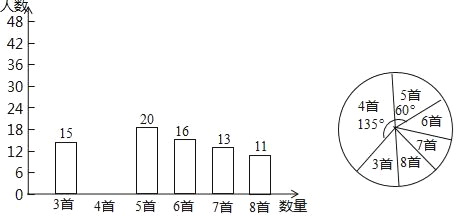
大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”,绘制成统计表
一周诗词诵背数量 | 3首 | 4首 | 5首 | 6首 | 7首 | 8首 |
人数 | 10 | 10 | 15 | 40 | 25 | 20 |
请根据调查的信息
(1)活动启动之初学生“一周诗词诵背数量”的中位数为 ;
(2)估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数;
(3)选择适当的统计量,从两个不同的角度分析两次调查的相关数据,评价该校经典诗词诵背系列活动的效果.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,点E在边AD上(不与点A、D重合),∠CEB=45°,EB与对角线AC相交于点F,设DE=x.
(1)用含x的代数式表示线段CF的长;
(2)如果把△CAE的周长记作C△CAE,△BAF的周长记作C△BAF,设![]() =y,求y关于x的函数关系式,并写出它的定义域;
=y,求y关于x的函数关系式,并写出它的定义域;
(3)当∠ABE的正切值是![]() 时,求AB的长.
时,求AB的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com