
科目: 来源: 题型:
【题目】如图,在矩形ABCD中,E是对角线BD上一点(不与点B、D重合),过点E作EF∥AB,且EF=AB,连接AE、BF、CF。
(1)若DE=DC,求证:四边形CDEF是菱形;
(2)若AB=![]() ,BC=3,当四边形ABFE周长最小时,四边形CDEF的周长为__________。
,BC=3,当四边形ABFE周长最小时,四边形CDEF的周长为__________。

查看答案和解析>>
科目: 来源: 题型:
【题目】某气球内充满了一定量的气体,当温度不变时,气球内气体的气压P(kPa)是气球体积V(m3)的反比例函数,且当V=0.8m3时,P=120kPa。
(1)求P与V之间的函数表达式;
(2)当气球内的气压大于100kPa时,气球将爆炸,为确保气球不爆炸,气球的体积应不小于多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知平面直角坐标系![]() (如图),直线
(如图),直线![]() 的经过点
的经过点![]() 和点
和点![]() .
.
(1)求![]() 、
、![]() 的值;
的值;
(2)如果抛物线![]() 经过点
经过点![]() 、
、![]() ,该抛物线的顶点为点
,该抛物线的顶点为点![]() ,求
,求![]() 的值;
的值;
(3)设点![]() 在直线
在直线![]() 上,且在第一象限内,直线
上,且在第一象限内,直线![]() 与
与![]() 轴的交点为点
轴的交点为点![]() ,如果
,如果![]() ,求点
,求点![]() 的坐标.
的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】学校开展“书香校园,诵读经典”活动,随机抽查了部分学生,对他们每天的课外阅读时长进行统计,并将结果分为四类:设每天阅读时长为t分钟,当0<t≤20时记为A类,当20<t≤40时记为B类,当40<t≤60时记为C类,当t>60时记为D类,收集的数据绘制成如下两幅不完整的统计图,请根据图中提供的信息,解答下列问题:

(1)这次共抽取了 名学生进行调查统计,扇形统计图中的D类所对应的扇形圆心角为 °;
(2)将条形统计图补充完整;
(3)若该校共有2000名学生,请估计该校每天阅读时长超过40分钟的学生约有多少人?
查看答案和解析>>
科目: 来源: 题型:
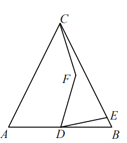
【题目】如图,△ABC是边长为6的等边三角形,D是AB中点,E是边BC上一动点,连结DE,将DE绕点D逆时针旋转60°得DF,连接CF,若CF=![]() ,则BE=_________。
,则BE=_________。
查看答案和解析>>
科目: 来源: 题型:
【题目】甲乙两地相距180km,一列慢车以40km/h的速度从甲地匀速驶往乙地,慢车出发30分钟后,一列快车以60km/h的速度从甲地匀速驶往乙地.两车相继到达终点乙地,再次过程中,两车恰好相距10km的次数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目: 来源: 题型:
【题目】有一座抛物线拱型桥,在正常水位时,水面![]() 的宽为
的宽为![]() 米,拱桥的最高点
米,拱桥的最高点![]() 到水面
到水面![]() 的距离
的距离![]() 为
为![]() 米,点
米,点![]() 是
是![]() 的中点,如图,以点
的中点,如图,以点![]() 为原点,直线
为原点,直线![]() 为
为![]() 轴,建立直角坐标系
轴,建立直角坐标系![]() .
.
(1)求该抛物线的表达式;
(2)如果水面![]() 上升
上升![]() 米(即
米(即![]() )至水面
)至水面![]() ,点
,点![]() 在点
在点![]() 的左侧,
的左侧,
求水面宽度![]() 的长.
的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】列分式方程解应用题:仔细阅读《战鸽总动员》中的对话,并回答问题,根据对话内容判断,小B超过最高时速了吗?为什么?
你们的任务是每人带一封信飞到离此地800km的我军基地,为安全起见,最快不能超过时速130km/h.
小B:虽然我的时速快,但最大时速也只比平均速度快20km/h,不知我最快时是否安全.
小V:你的速度太快了,平均每小时比我多飞25%,少用我2小时就飞完了全程,我要加紧练习才行,你也要注意安全.
查看答案和解析>>
科目: 来源: 题型:
【题目】学生参加植树造林,甲班每天比乙班多植5棵树,甲班植80棵树与乙班植70棵树所用的天数相等,求甲、乙两班每天各植树多少棵。下面列式错误的是 ( )
A.设甲班每天植树x棵,则![]() B.设乙班每天植树x棵,则
B.设乙班每天植树x棵,则![]()
C.设甲班在x天植树80棵,则![]() D.设乙班在x天植树70棵,则
D.设乙班在x天植树70棵,则![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知∠1=∠2,DE⊥BC,AB⊥BC,求证:∠A=∠3.
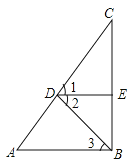
证明:∵ DE⊥BC,AB⊥BC(已知)
∴∠DEC=∠ABC=90°( )
∴DE∥AB(_________ ___)
∴∠2=____ (__________ ___________)
∠1= (____________ _________)
又∵∠1=∠2(_____________________)
∴∠A=∠3(_____________________)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com