
科目: 来源: 题型:
【题目】如图,将矩形纸片ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,连接AE.
求证:(1)BF=DF;
(2)若AB=6,AD=8,求BF的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图 ,已知B C=90 ,AEED,ABCE ,点F是AD的中点.说明EF与AD垂直的理由.
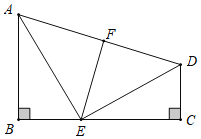
解:因为 AEED (已知),
所以AED=90 (垂直的意义).
因为AECBBAE ( ),
即AEDDECBBAE .
又因为B=90 (已知),
所以BAECED (等式性质).
在△ ABE 与△ ECD 中,
BC(已知),ABEC(已知),BAECED,
所以△ ABE≌△ECD ( ),
得 ( 全等三角形的对应边相等),
所以△AED 是等腰三角形.
因为 (已知),
所以 EFAD ( ).
查看答案和解析>>
科目: 来源: 题型:
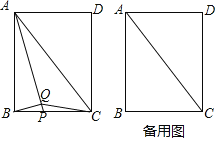
【题目】如图,在矩形![]() 中,
中,![]() 为对角线,点
为对角线,点![]() 为
为![]() 边上一动点,连结
边上一动点,连结![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连结
,连结![]() .
.
(1)证明:![]() ;
;
(2)当点![]() 为
为![]() 的中点时,若
的中点时,若![]() ,求
,求![]() 的度数;
的度数;
(3)当点![]() 运动到与点
运动到与点![]() 重合时,延长
重合时,延长![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,则
,则![]() .
.
查看答案和解析>>
科目: 来源: 题型:
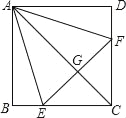
【题目】如图,正方形ABCD中,点E,F分别在BC,CD上,三角形AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF,②AG=2GC,③BE+DF=EF,④S△CEF=2S△ABE正确的有_____(只填序号).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFMN的一边MN在边BC上,顶点E、F分别在AB、AC上,其中BC=24cm,高AD=12cm.
(1)求证:△AEF∽△ABC:
(2)求正方形EFMN的边长.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.
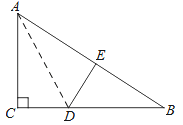
(1)求证:△BDE∽△BAC;
(2)已知AC=6,BC=8,求线段AD的长度.
查看答案和解析>>
科目: 来源: 题型:
【题目】数![]() 、b在数轴上的位置如图所示,
、b在数轴上的位置如图所示,
![]()
(1) a+b 0 , a-b 0; (填“>”、“=”或“<”)
(2) 化简:|a|-|b|+|a-b|
(3)在数轴上表示a+b与a-b;并把![]() 、b、0、a+b、a-b按从小到的顺序用“<”连接起来。
、b、0、a+b、a-b按从小到的顺序用“<”连接起来。
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在△ABC中,∠A=30°,点P从点A出发以2cm/s的速度沿折线A﹣C﹣B运动,点Q从点A出发以a(cm/s)的速度沿AB运动,P,Q两点同时出发,当某一点运动到点B时,两点同时停止运动.设运动时间为x(s),△APQ的面积为y(cm2),y关于x的函数图象由C1,C2两段组成,如图2所示.
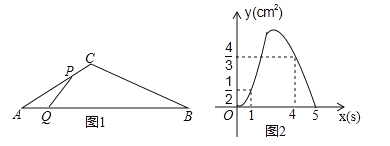
(1)求a的值;
(2)求图2中图象C2段的函数表达式;
(3)当点P运动到线段BC上某一段时△APQ的面积,大于当点P在线段AC上任意一点时△APQ的面积,求x的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知抛物线y=![]() x2+mx+n与x轴相交于点A、B两点,过点B的直线y=x+b交抛物线于另一点C(-5,6),点D是线段BC上的一个动点(点D与点B、C不重合),作DE∥AC,交该抛物线于点E,
x2+mx+n与x轴相交于点A、B两点,过点B的直线y=x+b交抛物线于另一点C(-5,6),点D是线段BC上的一个动点(点D与点B、C不重合),作DE∥AC,交该抛物线于点E,
(1)求m,n,b的值;
(2)求tan∠ACB;
(3)探究在点D运动过程中,是否存在∠DEA=45°,若存在,则求此时线段AE的长;若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】 为满足社区居民健身的需要,市政府准备采购若干套健身器材免费提供给社区,经考察,劲松公司有![]() 两种型号的健身器可供选择.
两种型号的健身器可供选择.
(1)劲松公司2015年每套![]() 型健身器的售价为
型健身器的售价为![]() 万元,经过连续两年降价,2017年每套售价为
万元,经过连续两年降价,2017年每套售价为![]() 万元,求每套
万元,求每套![]() 型健身器年平均下降率
型健身器年平均下降率![]() ;
;
(2)2017年市政府经过招标,决定年内采购并安装劲松公司![]() 两种型号的健身器材共
两种型号的健身器材共![]() 套,采购专项费总计不超过
套,采购专项费总计不超过![]() 万元,采购合同规定:每套
万元,采购合同规定:每套![]() 型健身器售价为
型健身器售价为![]() 万元,每套
万元,每套![]() 型健身器售价我
型健身器售价我![]() 万元.
万元.
①![]() 型健身器最多可购买多少套?
型健身器最多可购买多少套?
②安装完成后,若每套![]() 型和
型和![]() 型健身器一年的养护费分别是购买价的
型健身器一年的养护费分别是购买价的![]() 和
和![]() .市政府计划支出
.市政府计划支出![]() 万元进行养护.问该计划支出能否满足一年的养护需要?
万元进行养护.问该计划支出能否满足一年的养护需要?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com