练习册

  • 练习册
  • 试题
    相关习题
     0  355392  355400  355406  355410  355416  355418  355422  355428  355430  355436  355442  355446  355448  355452  355458  355460  355466  355470  355472  355476  355478  355482  355484  355486  355487  355488  355490  355491  355492  355494  355496  355500  355502  355506  355508  355512  355518  355520  355526  355530  355532  355536  355542  355548  355550  355556  355560  355562  355568  355572  355578  355586  366461 

    科目： 来源： 题型：

    【题目】如图，已知OE是∠AOC的角平分线，OD是∠BOC的角平分线．

    （1）若∠AOC=120°，∠BOC=30°，求∠DOE的度数；

    （2）若∠AOB=90°，∠BOC=α，求∠DOE的度数．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】下列说法中,正确的是( )

    A.单项式 的系数是-2，次数是3B.单项式a的系数是0，次数是0

    C.是三次三项式，常数项是1D.单项式的次数是2，系数为

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】某学校抽查了某班级某月10天的用电量，数据如下表：

    用电量/度

    8

    9

    10

    13

    14

    15

    天数

    1

    1

    2

    3

    1

    2

    （1）这10天用电量的众数是______度，中位数是______度；

    （2）求这个班级平均每天的用电量；

    （3）该校共有20个班级，该月共计30天，试估计该校该月总的用电量.

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】如图，在△ABC中，∠A＝m°，∠ABC和∠ACD的平分线相交于点A1，得∠A1；∠A1BC和∠A1CD的平分线相交于点A2，得∠A2；…；∠A2018BC和∠A2018CD的平分线交于点A2019，则∠A2019＝________度．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】已知数轴上的A、B两点分别对应数字a、b，且a、b满足|4a-b|+（a-4）2=0

    （1）a= ，b= ，并在数轴上面出A、B两点；

    （2）若点P从点A出发，以每秒3个单位长度向x轴正半轴运动，求运动时间为多少时，点P到点A的距离是点P到点B距离的2倍；

    （3）数轴上还有一点C的坐标为30，若点P和点Q同时从点A和点B出发，分别以每秒3个单位长度和每秒1个单位长度的速度向C点运动，P点到达C点后，再立刻以同样的速度返回，运动到终点A．求点P和点Q运动多少秒时，P、Q两点之间的距离为4，并求此时点Q对应的数．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】如图，平分，于点，于点，，则图中全等三角形的对数有______对.

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】如图①所示是一个长为2m，宽为2n的长方形，沿图中虚线用剪刀均分成四个小长方形，然后按图②的方式拼成一个正方形．

    （1）你认为图②中的阴影部分的正方形的边长等于_________________；

    （2）请用两种不同的方法列代数式表示图②中阴影部分的面积．

    方法① __________________．方法② _____________________；

    （3）观察图②，你能写出(m+n)2，(m-n)2，mn这三个代数式之间的等量关系吗？

    答：________________________ .

    （4）根据（3）题中的等量关系，解决如下问题：若a+b=6，ab=4，则求(a-b)2的值．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】如图,在△ABC中,P为BC上一点,PR⊥AB,垂足为R,PS⊥AC,垂足为S,∠CAP=∠APQ,PR=PS,下面的结论:①AS=AR;②QP∥AR;③△BRP≌△CSP.其中正确的是(　　)

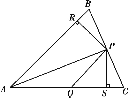
    A. ①② B. ②③ C. ①③ D. ①②③

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】规定：[x]表示不大于x的最大整数，（x）表示不小于x的最小整数，[x）表示最接近x的整数（x≠n+0.5，n为整数），例如：[2.3]=2，（2.3）=3，[2.3）=2．当﹣1＜x＜1时，化简 [x]+（x）+[x）的结果是__________________．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】在“宏扬传统文化，打造书香校园”活动中，学校计划开展四项活动：“A﹣国学诵读”、“B﹣演讲”、“C﹣课本剧”、“D﹣书法”，要求每位同学必须且只能参加其中一项活动，学校为了了解学生的意愿，随机调查了部分学生，结果统计如下：

    （1）如图，希望参加活动C占20%，希望参加活动B占15%，则被调查的总人数为 人，扇形统计图中，希望参加活动D所占圆心角为 度，根据题中信息补全条形统计图．

    （2）学校现有800名学生，请根据图中信息，估算全校学生希望参加活动A有多少人？

    查看答案和解析>>

    同步练习册答案