【题目】如图1，2分别是某款篮球架的实物图与示意图，已知底座BC=0.60米，底座BC与支架AC所成的角∠ACB=75°，支架AF的长为2.50米，篮板顶端F点到篮框D的距离FD=1.35米，篮板底部支架HE与支架AF所成的角∠FHE=60°，求篮框D到地面的距离（精确到0.01米）（参考数据：cos75°≈0.2588，sin75°≈0.9659，tan75°≈3.732，≈1.732，≈1.414）

（1）表中的a＝　 　，b＝　 　；

（2）请将频数分布直方图补全；

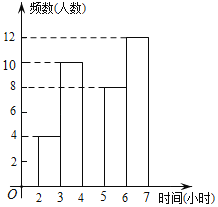
（3）若绘制扇形统计图，时间段6≤x＜7所对应扇形的圆心角的度数是多少？

（4）若该校共有1200名学生，估计全校每周在校参加体育锻炼时间至少有4小时的学生约为多少名？

【题目】1955年，印度数学家卡普耶卡（）研究了对四位自然数的一种变换：任给出四位数，用的四个数字由大到小重新排列成一个四位数，再减去它的反序数（即将的四个数字由小到大排列，规定反序后若左边数字有0，则将0去掉运算，比如0001，计算时按1计算），得出数，然后继续对重复上述变换，得数，…，如此进行下去，卡普耶卡发现，无论是多大的四位数，只要四个数字不全相同，最多进行次上述变换，就会出现变换前后相同的四位数，这个数称为变换的核.则四位数9631的变换的核为______.

(1)小明的站点，旗杆的接地点,标杆的接地点,三点应满足什么关系？

(2)在测量过程中,如果标杆的位置确定,小明应该通过移动位置，直到小明的视点与点 在同直一线上为止;

(3)他们都测得了哪些数据就能计算出旗杆的高度?请你用小写字母表示这些数据(不允许测量多余的数据)；

(4)请用(3)中的数据，直接表示出旗杆的高度.

（Ⅰ）解不等式：＜

（Ⅱ）解不等式组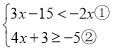

请结合题意填空，完成本题的解答；

（1）解不等式①，得：　 　；

（2）解不等式②，得：　 　；

（3）把不等式①和②的解集在如图数轴上表示出来；

（4）原不等式组的解集为　 　．

【题目】已知、在数轴上分别表示有理数，；

（1）对照数轴填写下表：

（2）若、两点间的距离记为，试问：和，有何数量关系？

（3）写出所有符合条件的整数点，使它到10和-10的距离之和为span>20，并求所有这些整数的数的和；

（4）找出（3）中满足到10和-10的距离之差大于1而小于5的整数的点；

（5）若点表示的数为，当点在什么位置时，取得的值最小，并求出这个最小值.

【题目】今年四月份，某校在孝感市争创“全国文明城市” 活动中，组织全体学生参加了“弘扬孝感文化，争做文明学生”知识竞赛，赛后随机抽取了部分参赛学生的成绩，按得分划分成 六个等级，并绘制成如下两幅不完整的统计图表.

请根据图表提供的信息，解答下列问题：

（1）本次抽样调查样本容量为 ，表中： ， ；扇形统计图中， 等级对应的圆心角 等于 度；（4分=1分+1分+1分）

（2）该校决定从本次抽取的 等级学生（记为甲、乙、丙、丁）中，随机选择 名成为学校文明宣讲志愿者，请你用列表法或画树状图的方法，求恰好抽到甲和乙的概率.

(1)求实数k的取值范围；

(2)若x1，x2满足x12＋x22＝16＋x1x2，求实数k的值．

【题目】已知图甲是一个长为，宽为的长方形，沿图甲中虚线用剪刀均匀分成四小块长方形，然后按图乙的形状拼成一个正方形.

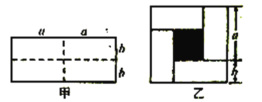
（1）求图乙中阴影部分正方形的边长（用含字母，的整式表示）；

（2）请用两种不同的方法求图乙中阴影部分的面积.

（3）观察图乙，并结合（2）中的结论，写出下列三个整式：，，之间的等量关系；

（4）根据（3）题中的等量关系，解决如下问题：若，，求的值.