
科目: 来源: 题型:
【题目】在一次科技作品制作比赛中,某小组8件作品的成绩(单位:分)分别是:7、10、9、8、7、9、9、8,对这组数据,下列说法正确的是( )
A. 众数是9B. 中位数是8C. 平均数是8D. 方差是7
查看答案和解析>>
科目: 来源: 题型:
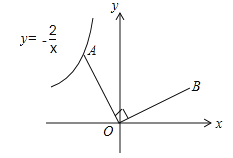
【题目】如图,已知点A是反比例函数![]() 的图象上的一个动点,连接OA,若将线段O A绕点O顺时针旋转90°得到线段OB,则点B所在图象的函数表达式为______.
的图象上的一个动点,连接OA,若将线段O A绕点O顺时针旋转90°得到线段OB,则点B所在图象的函数表达式为______.
查看答案和解析>>
科目: 来源: 题型:
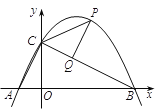
【题目】如图,二次函数y=ax2+bx+2![]() 的图像与y轴交于C点,交x轴于点A(-2,0),B(6,0).
的图像与y轴交于C点,交x轴于点A(-2,0),B(6,0).
⑴ 求该二次函数的表达式;
⑵ P是该函数在第一象限内图像上的动点,过点P作PQ⊥BC于点Q,连接PC、AC.
① 求线段PQ的最大值;
② 若以点P、C、Q为顶点的三角形与△ACO相似,求P点的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】⑴ 阅读理解:我们知道在直角三角形中,有无数组勾股数,例如:5、12、13;9、40、41;……但其中也有一些特殊的勾股数,例如:3、4、5;是三个连续正整数组成的勾股数.
解决问题:① 在无数组勾股数中,是否存在三个连续偶数能组成勾股数?
答: ,若存在,试写出一组勾股数: .
② 在无数组勾股数中,是否还存在其它的三个连续正整数能组成勾股数?若存在,求出勾股数,若不存在,说明理由.
③ 在无数组勾股数中,是否存在三个连续奇数能组成勾股数?若存在,求出勾股数,若不存在,说明理由.
⑵ 探索升华:是否存在锐角△ABC三边也为连续正整数;且同时还满足:∠B>∠C>∠A;∠ABC=2∠BAC?若存在,求出△ABC三边的长;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】公园门票价格规定如下表:
购票张数 | 1~50张 | 51~100张 | 100张以上 |
每张票的价格 | 15元 | 13元 | 11元 |
某校七年级(1)(2)两个班共102人去游园,其中(1)班超过40人,不足50人,经估算,如果两个班都以班为单位购票,则一共应付1422元.问:
(1)两个班各有多少学生?
(2)如果两个班联合起来,作为一个团体购票,可比两个班都以班为单位购票省多少元钱?
(2)如果七年级(1)班单独组织去游园,作为组织者的你如何购票才最省钱?
查看答案和解析>>
科目: 来源: 题型:
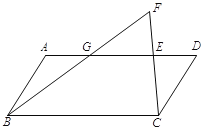
【题目】如图,□ABCD中,∠ABC为锐角,AB<BC,点E是AD上的一点,延长CE到F,连接BF交AD于点G, 使∠FBC=∠DCE.
⑴ 求证:∠D=∠F;
⑵ 在直线AD找一点P,使以点B、P、C为顶点的三角形与以点C、D、P为顶点的三角形相似.(在原图中标出准确P点的位置,必要时用直尺和圆规作出P点,保留作图的痕迹,不写作法)
查看答案和解析>>
科目: 来源: 题型:
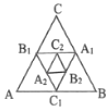
【题目】如图,点A1、B1、C1分别为△ABC的边BC、CA、AB的中点,点A2、B2、C2分别为△A1B1C1的边B1C1、C1A1、A1B1的中点,若△ABC的面积为1,则△A2B2C2的面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
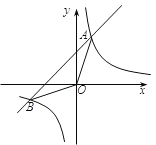
【题目】如图,反比例函数![]() 的图像与一次函数
的图像与一次函数![]() 的图像交于两点A(1,3),B(n,-1).
的图像交于两点A(1,3),B(n,-1).
⑴ k= ,n= ;
⑵ 求一次函数的表达式;
⑶ 结合图像直接回答:不等式![]() <mx+b解集是 ;
<mx+b解集是 ;
⑷ 求△AOB的面积.
查看答案和解析>>
科目: 来源: 题型:
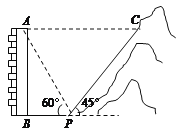
【题目】如图,一居民楼底部B与山脚P位于同一水平线上,小李在P处测得居民楼顶A的仰角为60°,然后他从P处沿坡角为45°的山坡向上走到C处,这时,PC=30 m,点C与点A恰好在同一水平线上,点A、B、P、C在同一平面内.
(1)求居民楼AB的高度;
(2)求C、A之间的距离.(结果保留根号)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,∠MAN=30°,点O为边AN上一点,以O为圆心,4为半径
作⊙O交AN于D、E两点.
⑴ 当⊙O与AM相切时,求AD的长;
⑵ 如果AD=2,那么AM与⊙O又会有怎样的位置关系?并说明理由.
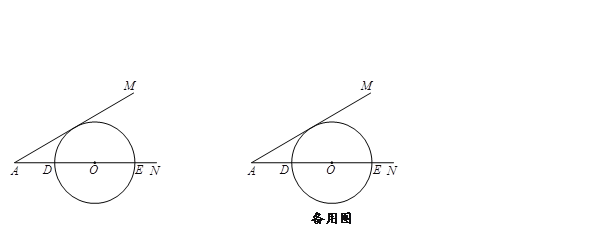
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com