
科目: 来源: 题型:
【题目】一位农民带上若干千克自产的土豆进城出售.为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数x与他手中持有的钱数y(含备用零钱)的关系如图所示,结合图象回答下列问题:

(1)农民自带的零钱是多少?
(2)求降价前农民手中的钱数y与售出的土豆千克数x的函数关系式;
(3)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,试问他一共带了多少千克土豆?
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下面材料:
小明遇到这样一个问题:如图1,在![]() 中和
中和![]() 中,
中,![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .求证:
.求证:![]() .
.
小明经探究发现,过![]() 点作
点作![]() ,交
,交![]() 于点
于点![]() (如图2),从而可证
(如图2),从而可证![]() ,使问题得到解决.
,使问题得到解决.
(1)请你按照小明单独探究思路,完成他的证明过程;
参考小明思考问题的方法,解决下面的问题:
(2)如图3,在![]() 与
与![]() 中,
中,![]() 分别为
分别为![]() 、
、![]() 的中线,连接
的中线,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,是否存在与
,是否存在与![]() 相等的线段?若存在,请找出并证明;若不存在,说明理由.
相等的线段?若存在,请找出并证明;若不存在,说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】老师和小明同学玩数学游戏.老师取出一个不透明的口袋,口袋中装有三张分别标有数字1,2,3的卡片,卡片除数字外其余都相同,老师要求小明同学两次随机抽取一张卡片,并计算两次抽到卡片上的数字之积是奇数的概率.于是小明同学用画树状图的方法寻求他两次抽取卡片的所有可能结果.如图是小明同学所画的正确树状图的一部分.
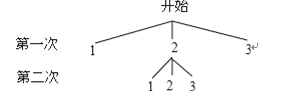
(1)补全小明同学所画的树状图;
(2)求小明同学两次抽到卡片上的数字之积是奇数的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,它表示甲乙两人从同一个地点出发后的情况。到10:00时,甲大约走了13千米。根据图象回答:
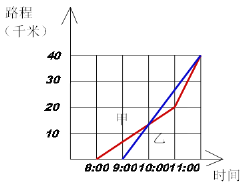
(1)甲是几点钟出发?
(2)乙是几点钟出发,到十点时,他大约走了多少千米?
(3)到10:00为止,哪个人的速度快?
(4)两人在途中有几次相遇?分别在几点钟相遇?
查看答案和解析>>
科目: 来源: 题型:
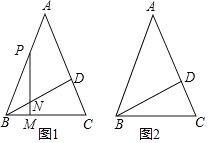
【题目】如图1,在等腰![]() 中,
中,![]() ,点
,点![]() 为边
为边![]() 上一点(不与点
上一点(不与点![]() 、点
、点![]() 重合),
重合),![]() ,垂足为
,垂足为![]() ,交
,交![]() 于点
于点![]() .
.
(1)请猜想![]() 与
与![]() 之间的数量关系,并证明;
之间的数量关系,并证明;
(2)若点![]() 为边
为边![]() 延长线上一点,
延长线上一点,![]() ,垂足为
,垂足为![]() ,交
,交![]() 延长线于点
延长线于点![]() ,请在图2中画出图形,并判断(1)中的结论是否成立.若成立,请证明;若不成立,请写出你的猜想并证明.
,请在图2中画出图形,并判断(1)中的结论是否成立.若成立,请证明;若不成立,请写出你的猜想并证明.
查看答案和解析>>
科目: 来源: 题型:
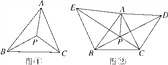
【题目】如图①,P为△ABC所在平面上一点,且∠APB=∠BPC=∠CPA=120°,则点P叫作△ABC的费马点.
(1)如果点P为锐角△ABC的费马点,且∠ABC=60°.
①求证: △ABP∽△BCP;
②若PA=3,PC=4,求PB的长;
(2)如图②,已知锐角△ABC,分别以AB,AC为边向外作正△ABE和正△ACD,CE和BD相交于点P,连接AP.
①求∠CPD的度数;
②求证:点P为△ABC的费马点.
查看答案和解析>>
科目: 来源: 题型:
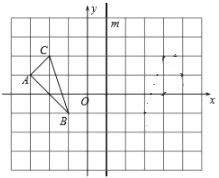
【题目】如图,在平面直角坐标系中,![]() 的顶点坐标分别为
的顶点坐标分别为![]() 、
、![]() 、
、![]() .
.
(1)不用画图,请直接写出![]() 关于
关于![]() 轴对称的图形
轴对称的图形![]() 的三个顶点的坐标:
的三个顶点的坐标:![]() ,
,![]() ,
,![]() ;
;
(2)在图中画出![]() 关于直线
关于直线![]() (直线
(直线![]() 上各点的横坐标都为1)对称的图形
上各点的横坐标都为1)对称的图形![]() ,并直接写出三个顶点的坐标:
,并直接写出三个顶点的坐标:![]() ,
,![]() ,
,![]() ;
;
(3)若![]() 内有任意一点
内有任意一点![]() 的坐标为
的坐标为![]() ,则在
,则在![]() 关于直线
关于直线![]() (直线
(直线![]() 上各点的横坐标都为1)对称的图形
上各点的横坐标都为1)对称的图形![]() 上,点
上,点![]() 的对应点
的对应点![]() 的坐标 .(用含
的坐标 .(用含![]() 和
和![]() 的式子表示)
的式子表示)
(建议:先用铅笔画图,确定无误后用黑色水性笔画在答题卡上)
查看答案和解析>>
科目: 来源: 题型:
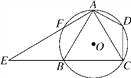
【题目】如图,已知四边形ABCD内接于⊙O,A是![]() 的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F,E,且
的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F,E,且![]() .
.
(1)求证:△ADC∽△EBA;
(2)如果AB=8,CD=5,求tan∠CAD的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com