
科目: 来源: 题型:
【题目】如图,把一个边长为a的正方形分成9个完全相同的小正方形,把最中间的一个小正方形涂成白色(图①),再对其他8个小正方形作同样的分割(分成9个完全相同的小正方形,把最中间的一个小正方形涂成白色(图②),继续同样的方法分割图形(图③),…得到一些既复杂又漂亮的图形,它的每一部分放大,都和整体一模一样,它是波兰数学家谢尔宾斯基构造的,也被称为“谢尔宾斯基地毯”.求:
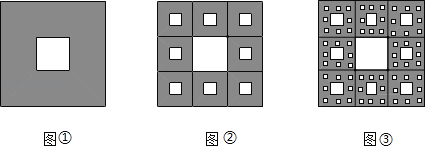
(1)图③中最新的一个最小正方形的边长;
(2)图③中所有涂黑部分的面积.
查看答案和解析>>
科目: 来源: 题型:
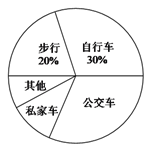
【题目】某校为了解全校2400名学生到校上学的方式,在全校随机抽取了若干名学生进行问卷调查.问卷给出了五种上学方式供学生选择,每人只能选一项,且不能不选.将调查得到的结果绘制成如图所示的频数分布直方图和扇形统计图(均不完整).
(1)这次调查中,一共抽取了多少名学生?
(2)补全频数分布直方图;
(3)估计全校所有学生中有多少人乘坐公交车上学.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四边形ABCD中,点E在边CD上,连结AE、BE.给出下列五个关系式:①AD∥BC;②DE=CE;③∠1=∠2;④∠3=∠4;⑤AD+BC=AB.将其中的三个关系式作为题设,另外两个作为结论,构成一个命题.
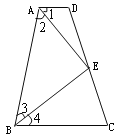
⑴用序号写出一个真命题(书写形式如:如果×××,那么××);并给出证明;
⑵用序号再写出三个真命题(不要求证明)
查看答案和解析>>
科目: 来源: 题型:
【题目】某同学准备购买笔和本子送给农村希望小学的同学,在市场上了解到购买某种本子30个和某种笔10支共需280元;购买某种本子50个和某种笔20枝共需500元。
(1)求这种本子和笔的单价;
(2)该同学打算用自己的100元压岁钱购买这种笔和本子,计划100元刚好用完,并且笔和本子都买,请列出所有购买方案.
查看答案和解析>>
科目: 来源: 题型:
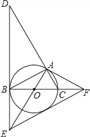
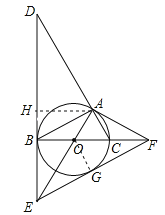
【题目】如图,⊙O是△ABC的外接圆,BC是⊙O的直径,∠ABC=30°,过点B作⊙O的切线BD,与CA的延长线交于点D,与半径AO的延长线交于点E,过点A作⊙O的切线AF,与直径BC的延长线交于点F.
(1)求证:△ACF∽△DAE;
(2)若S△AOC=![]() ,求DE的长;
,求DE的长;
(3)连接EF,求证:EF是⊙O的切线.
【答案】(1) 见解析; (2)3![]() ;(3)见解析.
;(3)见解析.
【解析】试题分析:(1)根据圆周角定理得到∠BAC=90°,根据三角形的内角和得到∠ACB=60°根据切线的性质得到∠OAF=90°,∠DBC=90°,于是得到∠D=∠AFC=30°由相似三角形的判定定理即可得到结论;
(2)根据S△AOC=![]() ,得到S△ACF=
,得到S△ACF=![]() ,通过△ACF∽△DAE,求得S△DAE=
,通过△ACF∽△DAE,求得S△DAE=![]() ,过A作AH⊥DE于H,解直角三角形得到AH=
,过A作AH⊥DE于H,解直角三角形得到AH=![]() DH=
DH=![]() DE,由三角形的面积公式列方程即可得到结论;
DE,由三角形的面积公式列方程即可得到结论;
(3)根据全等三角形的性质得到OE=OF,根据等腰三角形的性质得到∠OFG=![]() (180°﹣∠EOF)=30°,于是得到∠AFO=∠GFO,过O作OG⊥EF于G,根据全等三角形的性质得到OG=OA,即可得到结论.
(180°﹣∠EOF)=30°,于是得到∠AFO=∠GFO,过O作OG⊥EF于G,根据全等三角形的性质得到OG=OA,即可得到结论.
试题解析:(1)证明:∵BC是⊙O的直径,∴∠BAC=90°,∵∠ABC=30°,∴∠ACB=60°
∵OA=OC,∴∠AOC=60°,∵AF是⊙O的切线,∴∠OAF=90°,∴∠AFC=30°,∵DE是⊙O的切线,∴∠DBC=90°,∴∠D=∠AFC=30,∵∠DAE=ACF=120°,∴△ACF∽△DAE;
(2)∵∠ACO=∠AFC+∠CAF=30°+∠CAF=60°,∴∠CAF=30°,∴∠CAF=∠AFC,∴AC=CF,∴OC=CF,∵S△AOC=![]() ,∴S△ACF=
,∴S△ACF=![]() ,∵∠ABC=∠AFC=30°,∴AB=AF,∵AB=
,∵∠ABC=∠AFC=30°,∴AB=AF,∵AB=![]() BD,∴AF=
BD,∴AF=![]() BD,∴∠BAE=∠BEA=30°,∴AB=BE=AF,∴
BD,∴∠BAE=∠BEA=30°,∴AB=BE=AF,∴![]() ,∵△ACF∽△DAE,∴
,∵△ACF∽△DAE,∴![]() =
=![]() ,∴S△DAE=
,∴S△DAE=![]() ,过A作AH⊥DE于H,∴AH=
,过A作AH⊥DE于H,∴AH=![]() DH=
DH=![]() DE,∴S△ADE=
DE,∴S△ADE=![]() DEAH=
DEAH=![]() ×
×![]()
![]() =
=![]() ,∴DE=
,∴DE=![]() ;
;
(3)∵∠EOF=∠AOB=120°,∴∠OEB=∠AFO,在△AOF与△BOE中,∵∠OBE=∠OAF,∠OEB=∠AFO,OA=OB,∴△AOF≌△BEO,∴OE=OF,∴∠OFG=![]() (180°﹣∠EOF)=30°,∴∠AFO=∠GFO,过O作OG⊥EF于G,∴∠OAF=∠OGF=90°,在△AOF与△OGF中,∵∠OAF=∠OGF,∠AFO=∠GFO,OF=OF,∴△AOF≌△GOF,∴OG=OA,∴EF是⊙O的切线.
(180°﹣∠EOF)=30°,∴∠AFO=∠GFO,过O作OG⊥EF于G,∴∠OAF=∠OGF=90°,在△AOF与△OGF中,∵∠OAF=∠OGF,∠AFO=∠GFO,OF=OF,∴△AOF≌△GOF,∴OG=OA,∴EF是⊙O的切线.
【题型】解答题
【结束】
25
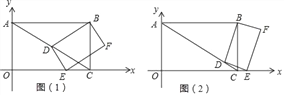
【题目】如图,在平面直角坐标系中,O为原点,四边形ABCO是矩形,点A,C的坐标分别是A(0,2)和C(2![]() ,0),点D是对角线AC上一动点(不与A,C重合),连结BD,作DE⊥DB,交x轴于点E,以线段DE,DB为邻边作矩形BDEF.
,0),点D是对角线AC上一动点(不与A,C重合),连结BD,作DE⊥DB,交x轴于点E,以线段DE,DB为邻边作矩形BDEF.
(1)填空:点B的坐标为 ;
(2)是否存在这样的点D,使得△DEC是等腰三角形?若存在,请求出AD的长度;若不存在,请说明理由;
(3)①求证:![]() ;
;
②设AD=x,矩形BDEF的面积为y,求y关于x的函数关系式(可利用①的结论),并求出y的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】定义一种对正整数n的“F运算”:①当n为奇数时,结果为3n+5;②当n为偶数时,结果为![]() (其中k是使
(其中k是使![]() 为奇数的正整数),并且运算重复进行,例如,取n=26,第三次“F运算”的结果是11.若n=111,则第2019次“F运算”的结果是_____.
为奇数的正整数),并且运算重复进行,例如,取n=26,第三次“F运算”的结果是11.若n=111,则第2019次“F运算”的结果是_____.
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC=_______.

查看答案和解析>>
科目: 来源: 题型:
【题目】下列结论:①几个有理数相乘,若其中负因数有奇数个,则积为负;②两个三次多项式的和一定是三次多项式;③若xyz<0,则![]() +
+![]() +
+![]() +
+![]() 的值为0或﹣4;④若a,b互为相反数,则
的值为0或﹣4;④若a,b互为相反数,则![]() =﹣1;⑤若x=y,则
=﹣1;⑤若x=y,则![]() =
=![]() .其中正确的个数有( )
.其中正确的个数有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目: 来源: 题型:
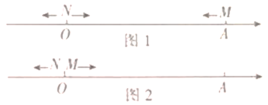
【题目】数轴上点A表示的数为10,点M,N分别以每秒a个单位长度,每秒b个单位长度的速度沿数轴运动,a, b满足|a-5|+(b-6)2=0.
(1)请真接与出a= , b= ;
(2)如图1,点M从A出发沿数轴向左运动,到达原点后立即返回向右运动:同时点N从原点0出发沿数轴向左运动,运动时间为t,点P为线段ON的中点若MP=MA,求t的值:
(3)如图2,若点M从原点向右运动,同时点N从原点向左运动,运动时间为t时M运动到点A的右侧,若此时以M,N, O, A为端点的所有线段的长度和为142,求此时点M对应的数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com