
科目: 来源: 题型:
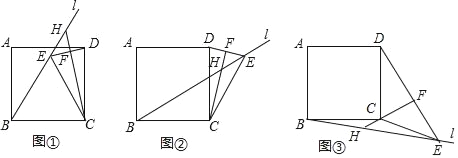
【题目】在正方形ABCD中,过点B作直线l,点E在直线l上,连接CE,DE,CE=BC,过点C作CF⊥DE于点F,交直线l于点H,当l在如图①的位置时,易证:BH+EH=![]() CH(不需证明).
CH(不需证明).
(1)当l在如图②的位置时,线段BH,EH,CH之间有怎样的数量关系?写出你的猜想,并给予证明;
(2)当l在如图③的位置时,线段BH,EH,CH之间有怎样的数量关系?写出你的猜想,不必证明.
查看答案和解析>>
科目: 来源: 题型:
【题目】在数轴上,点M、N表示的数分别为a、b,我们把a、b之差的绝对值叫做点M、N之间的距离,即MN=│a-b│.已知数轴上三点A、O、B表示的数分别为-3,0,1,点P为数轴上任意一点,其表示的数为x.
![]()
(1)如果点P到点A、点B的距离相等,那么x=_______;
(2)当x是多少时,点P到点A、点B的距离之和是6;
(3)若点P以每秒3个单位长度的速度从点O沿着数轴的负方向运动时,点E以每秒1个单位长度的速度从点A沿着数轴的负方向运动,点F以每秒4个单位长度的速度从点B沿着数轴的负方向运动,且三个点同时出发,那么运动几秒时,点P到点E、点F的距离相等.
查看答案和解析>>
科目: 来源: 题型:
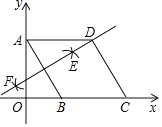
【题目】如图,在平面直角坐标系中,四边形ABCD是菱形,点A的坐标为(0,![]() ),分别以A,B为圆心,大于
),分别以A,B为圆心,大于![]() AB的长为半径作弧,两弧交于点E,F,直线EF恰好经过点D,则点D的坐标为( )
AB的长为半径作弧,两弧交于点E,F,直线EF恰好经过点D,则点D的坐标为( )
A. (2,2)B. (2,![]() )C. (
)C. (![]() ,2)D. (
,2)D. (![]() +1,
+1,![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】小明从家出发沿滨江路到外滩公园徒步锻炼,到外滩公园后立即沿原路返回,小明离开家的路程s(单位:千米)与走步时间t(单位:小时)之间的函数关系如图所示,其中从家到外滩公园的平均速度是4千米/时,根据图形提供的信息,解答下列问题:
(1)求图中的a值;
(2)若在距离小明家5千米处有一个地点C,小明从第一层经过点C到第二层经过点C,所用时间为1.75小时,求小明返回过程中,s与t的函数解析式,不必写出自变量的取值范围;
(3)在(2)的条件下,求小明从出发到回到家所用的时间.

查看答案和解析>>
科目: 来源: 题型:
【题目】在大课间活动中,同学们积极参加体育锻炼,小龙在全校随机抽取了一部分同学就“我最喜爱的体育项目”进行了一次调查(每位同学必选且只选一项).下面是他通过收集的数据绘制的两幅不完整的统计图,请你根据图中提供的信息,解答以下问题:
(1)小龙一共抽取了 名学生.
(2)补全条形统计图;
(3)求“其他”部分对应的扇形圆心角的度数.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,小贤为了体验四边形的不稳定性,将四根木条用钉子钉成一个矩形框架ABCD,B与D两点之间用一根橡皮筋拉直固定,然后向右扭动框架,观察所得四边形的变化,下列判断错误的是( )
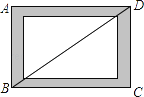
A. 四边形ABCD由矩形变为平行四边形 B. BD的长度增大
C. 四边形ABCD的面积不变 D. 四边形ABCD的周长不变
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A,B两点,且点A在点B的左侧,直线y=﹣x﹣1与抛物线交于A,C两点,其中点C的横坐标为2.
(1)求二次函数的解析式;
(2)P是线段AC上的一个动点,过点P作y轴的平行线交抛物线于点E,求线段PE长度的最大值.

查看答案和解析>>
科目: 来源: 题型:
【题目】目前节能灯在城市已基本普及,某商场计划购进甲、乙两种节能订共1200只,这两种节能灯的进价、售价如下表:
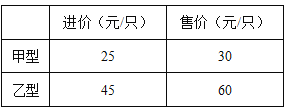
(1)如何进货,进货款恰好为46000元?
(2)为确保乙型节能灯顺利畅销,在(1)的条件下,商家决定对乙型节能灯进行打折出售,且全部售完后,乙型节能灯的利润率为20%,请同乙型节能灯需打几折?
查看答案和解析>>
科目: 来源: 题型:
【题目】某农科所对甲、乙两种小麦各选用10块面积相同的试验田进行种植试验,它们的平均亩产量分别是![]() =610千克,
=610千克,![]() =608千克,亩产量的方差分别是
=608千克,亩产量的方差分别是![]() ="29." 6,
="29." 6,![]() ="2." 7. 则关于两种小麦推广种植的合理决策是 ( )
="2." 7. 则关于两种小麦推广种植的合理决策是 ( )
A. 甲的平均亩产量较高,应推广甲
B. 甲、乙的平均亩产量相差不多,均可推广
C. 甲的平均亩产量较高,且亩产量比较稳定,应推广甲
D. 甲、乙的平均亩产量相差不多,但乙的亩产量比较稳定,应推广乙
查看答案和解析>>
科目: 来源: 题型:
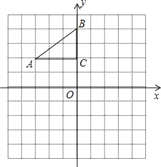
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;
(2)平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2 ;
(3)若将△A1B1C绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com