【题目】如图，已知△ABC是面积为4的等边三角形，△ABC∽△ADE，

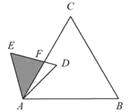
AB＝2AD，∠BAD＝45°，AC与DE相交于点F，则△AEF的面积

等于___（结果保留根号）．

【题目】如图，已知双曲线，经过点D（6，1），点C是双曲线第三象限上的动点，过C作CA⊥x轴，过D作DB⊥y轴，垂足分别为A，B，连接AB，BC．

（1）求k的值；

（2）若△BCD的面积为12，求直线CD的解析式；

（3）判断AB与CD的位置关系，并说明理由．

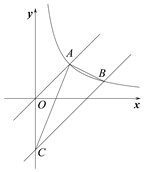
【题目】如图，直线OA与反比例函数()的图像交于点A(3，3)，将直线OA沿y轴向下平移，与反比例函数()的图像交于点B(6，m)，与y轴交于点C．

（1）求直线BC的解析式；

（2）求△ABC的面积．

【题目】小明家的洗手盆上装有一种抬启式水龙头（如图1），完全开启后，把手AM的仰角α=37°，此时把手端点A、出水口B和点落水点C在同一直线上，洗手盆及水龙头的相关数据如图2.（参考数据：sin37°=，cos37°=，tan37°=）

求把手端点A到BD的距离；

求CH的长.

解：∵O是直线AB上一点，∠AOC＝50°，

∴∠BOC＝180°－∠AOC＝ °.

∵ OD是∠BOC的角平分线，

∴∠COD＝ ∠BOC .( )

∴∠COD＝65°.

∵OE⊥OC于点O，（已知）.

∴∠COE＝ °.( )

∴∠DOE＝∠COE－∠COD＝ ° .

（1）求证：四边形 BFCE 是平行四边形．

（2）若 AD=10，EC=3，∠EBD=60°，当四边形 BFCE是菱形时，求 AB 的长．

【题目】如图，在平面直角坐标系中，四边形ABCD是矩形，AD∥x轴，A（，），AB=1，AD=2．

（1）直接写出B、C、D三点的坐标；

（2）将矩形ABCD向右平移m个单位，使点A、C恰好同时落在反比例函数（）的图象上，得矩形A′B′C′D′．求矩形ABCD的平移距离m和反比例函数的解析式．

如图1，△ABC为等边三角形，作AD⊥BC于点D，将∠ABC绕点B顺时针旋转30°后，BA，BC边与射线AD分别交于点E,F，求证：△BEF为等边三角形.

迁移应用：

如图2，△ABC为等边三角形，点P是△ABC外一点，∠BPC=60°，将∠BPC绕点P逆时针旋转60°后，PC边恰好经过点A，探究PA,PB,PC之间存在的数量关系，并证明你的结论；

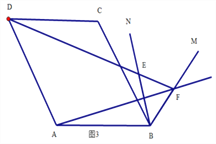
拓展延伸：

如图3，在菱形ABCD中，∠ABC=60°,将∠ABC绕点B顺时针旋转到如图所在的位置得到∠MBN，F是BM上一点，连接AF，DF，DF交BN于点E,若B,E两点恰好关于直线AF对称.

（1）证明△BEF是等边三角形；

（2）若DE=6,BE=2,求AF的长.