
科目: 来源: 题型:
【题目】某公司员工分别住在A、B、C三个住宅区,A区有25人,B区有15人,C区有10人,三个区在一条直线上,位置如图所示,公司的接送车打算在此间只设一个停靠点,为使所有员工步行到停靠点的路程总和最少,那么停靠点的位置应设在( )

A. A区 B. B区 C. A区或B区 D. C区
查看答案和解析>>
科目: 来源: 题型:
【题目】将连续的奇数1,3,5,7,9,…,2019,排成如图所示的数阵.十字框能上下左右移动,可框住5个数.

(1)如图,若十字框中间的数为25,这5个数的和是多少?
(2)设十字框中间的数为![]() ,用式子表示另外4个数.
,用式子表示另外4个数.
(3)框住的5个数的和能否等于2020,请说明理由.
(4)框住的5个数的和最大是多少?(给出结果,不说理由.)
查看答案和解析>>
科目: 来源: 题型:
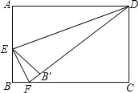
【题目】如图,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC上的动点,将△EBF沿EF所在直线折叠得到△EB′F,连接B′D,则B′D的最小值是( )
A. 2![]() ﹣2B. 6C. 2
﹣2B. 6C. 2![]() ﹣2D. 4
﹣2D. 4
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,A(﹣![]() ,0)、B(0,1)分别为x轴、y轴上的点,△ABC为等边三角形,点P(3,a)在第一象限内,且满足2S△ABP=S△ABC,则a的值为( )
,0)、B(0,1)分别为x轴、y轴上的点,△ABC为等边三角形,点P(3,a)在第一象限内,且满足2S△ABP=S△ABC,则a的值为( )

A.![]() B.
B.![]() C.
C.![]() D.2
D.2
查看答案和解析>>
科目: 来源: 题型:
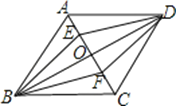
【题目】如图,O是菱形ABCD的对角线AC,BD的交点,E,F分别是OA,OC的中点.下列结论:①S△ADE=S△EOD;②四边形BFDE也是菱形;③△DEF是轴对称图形;④∠ADE=∠EDO;⑤四边形ABCD面积为EF×BD.其中正确的结论有( )
A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目: 来源: 题型:
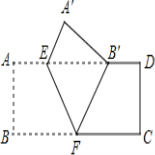
【题目】(2013年四川南充3分)如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是【 】
A.12 B. 24 C. 12![]() D. 16
D. 16![]()
查看答案和解析>>
科目: 来源: 题型:
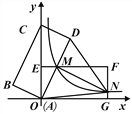
【题目】如图,矩形ABCD的顶点A在坐标原点,顶点C在y轴上,OB=2![]() 。将矩形ABCD绕点O顺时针旋转60°,使点D落在x轴的点G处,得到矩形AEFG,EF与AD交于点M,过点M的反比例函数图象交FG于点N,连接DN.
。将矩形ABCD绕点O顺时针旋转60°,使点D落在x轴的点G处,得到矩形AEFG,EF与AD交于点M,过点M的反比例函数图象交FG于点N,连接DN.
(1)求反比例函数的解析式
(2)求△AMN的面积;
查看答案和解析>>
科目: 来源: 题型:
【题目】为深化义务教育课程改革,满足学生的个性化学习需求,某校就“学生对知识拓展,体育特长、艺术特长和实践活动四类选课意向”进行了抽样调查(每人选报一类),绘制了如图所示的两幅统计图(不完整),请根据图中信息,解答下列问题:
(1)求扇形统计图中m的值,并补全条形统计图;
(2)在被调查的学生中,随机抽一人,抽到选“体育特长类”或“艺术特长类”的学生的概率是多少?

(3)已知该校有800名学生,计划开设“实践活动类”课程每班安排20人,问学校开设多少个“实践活动类”课程的班级比较合理?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图①,在平面直角坐标系中,A(a,0),C(b,2),且满足(a+2)2+![]() =0,过C作CB⊥x轴于B.
=0,过C作CB⊥x轴于B.
(1)求三角形ABC的面积;
(2)如图②,若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,求∠AED的度数;
(3)在y轴上是否存在点P,使得三角形ACP和三角形ABC的面积相等?若存在,求出P点的坐标;若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】实验中学捐资购买了一批物资240吨打算扶贫山区。现有甲、乙、丙三种车型可供选择,每辆车的运载能力和运费如下表所示(每辆车均装满)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨) | 10 | 16 | 20 |
汽车运费(元/辆) | 400 | 500 | 600 |
(1)若全部物资都用甲、乙两种车型来运送,需运费8200元。求甲、乙两种车型各多少辆?
(2)为了节约运费,该公司打算用甲、乙、丙三种车型同时参与运送,已知三种车辆总数为14辆。请求出三种车型分别是多少辆?此时的运费又是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com