
科目: 来源: 题型:
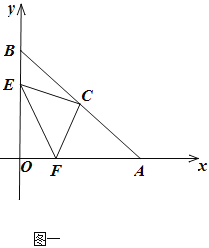
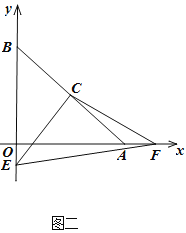
【题目】如图,RtΔOAB中,点O(0,0),点A(6,0),点B(0,6),斜边AB的中点C.
点E从点B出发,沿BO方向,点F从点O出发,沿OA方向,速度都是1个单位/秒,时间是t秒,连接CE、CF、EF,
(1)直接写出C点坐标______.
(2)判断ΔCEF的形状,并证明;
(3)在0<t<6时,以C、E、F、O四点组成的四边形面积是否发生变化?不变,求出这个值;变化,用含t的式子表示;
(4)在t>6时,以C、E、F、O四点组成的四边形面积是否发生变化?不变,求出这个值;变化,用含t的式子表示.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)如图1,点![]() 在线段
在线段![]() 上,
上,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() 的中点.求线段
的中点.求线段![]() 的长;
的长;

(2)点![]() 在线段
在线段![]() 上,若
上,若![]() ,点
,点![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() 的中点.你能得出
的中点.你能得出![]() 的长度吗?并说明理由.
的长度吗?并说明理由.
(3)类似的,如图2,![]() 是直角,射线
是直角,射线![]() 在
在![]() 外部,且
外部,且![]() 是锐角,
是锐角,![]() 是
是![]() 的平分线,
的平分线,![]() 是
是![]() 的平分线.当
的平分线.当![]() 的大小发生改变时,
的大小发生改变时,![]() 的大小也会发生改变吗?为什么?
的大小也会发生改变吗?为什么?
查看答案和解析>>
科目: 来源: 题型:
【题目】小张和同学相约“五一”节到离家2400米的电影院看电影,到电影院后,发现电影票忘带了,此时离电影开始还有25分钟,于是他跑步回家,拿到票后立刻找到一辆“共享单车”原路赶回电影院,已知小张骑车的时间比跑步的时间少用了4分钟,骑车的平均速度是跑步的平均速度的1.5倍.
(1)求小张跑步的平均速度;
(2)如果小张在家取票和寻找“共享单车”共用了6分钟,他能否在电影开始前赶到电影院?说明理由.
查看答案和解析>>
科目: 来源: 题型:
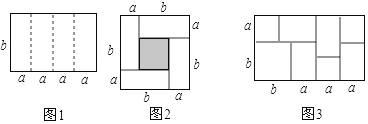
【题目】如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形(如图2)
(1)观察图2请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是_____;
(2)根据(1)中的结论,若x+y=5,xy=![]() ,则x﹣y=______;
,则x﹣y=______;
(3)若(3x﹣2y)2=5,(3x+2y)2=9,求xy的值.
(4)实际上通过计算图形的面积可以探求相应的等式.如图3,你有什么发现?_____.
查看答案和解析>>
科目: 来源: 题型:
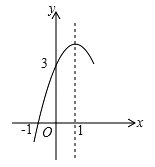
【题目】如图,抛物线![]() (a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:①4ac<b2; ②3a+c>0;③方程
(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:①4ac<b2; ②3a+c>0;③方程![]() 的两个根是x1=﹣1,x2=3;④当y>0时,x的取值范围是﹣1<x<3⑤当x>0时,y随x的增大而减小.其中结论正确的个数是( )
的两个根是x1=﹣1,x2=3;④当y>0时,x的取值范围是﹣1<x<3⑤当x>0时,y随x的增大而减小.其中结论正确的个数是( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目: 来源: 题型:
【题目】暖羊羊有5张写着不同数字的卡片,请你按要求选择卡片,完成下列各问题:
![]()
(1)从中选择两张卡片,使这两张卡片上数字的乘积最大.
这两张卡片上的数字分别是 ,积为 _.
(2)从中选择两张卡片,使这两张卡片上数字相除的商最小.
这两张卡片上的数字分别是 ,商为 .
(3)从中选择4张卡片,每张卡片上的数字只能用一次,选择加、减、乘、除中的适当方法(可加括号),使其运算结果为24,写出运算式子.(写出一种即可)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一个长5m的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为4m,如果梯子的顶端A沿墙下滑1m至C点.
(1)求梯子底端B外移距离BD的长度;
(2)猜想CE与BE的大小关系,并证明你的结论.

查看答案和解析>>
科目: 来源: 题型:
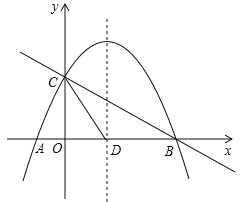
【题目】如图,抛物线![]() 与
与![]() 轴交于A、B两点,与
轴交于A、B两点,与![]() 轴交于点C,抛物线的对称轴交
轴交于点C,抛物线的对称轴交![]() 轴于点D,已知点A(-1,0),点C(0,2).
轴于点D,已知点A(-1,0),点C(0,2).
(1)求抛物线的函数解析式;
(2)线段BC上有一动点P,过点P作![]() 轴的平行线,交抛物线于点Q,求线段PQ的最大值;
轴的平行线,交抛物线于点Q,求线段PQ的最大值;
(3)若点E在![]() 轴上,点F在抛物线上.是否存在以C、D、E、F为顶点且以CD为一边的平行四边形?若存在,请你求出点F的坐标;若不存在,请说明理由.
轴上,点F在抛物线上.是否存在以C、D、E、F为顶点且以CD为一边的平行四边形?若存在,请你求出点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,D是边AC上的一点,连接BD,使∠A=2∠1,E是BC上的一点,以BE为直径的⊙O经过点D.

(1)求证:AC是⊙O的切线;
(2)若∠A=60°,⊙O的半径为2,求阴影部分的面积.(结果保留根号和π)
查看答案和解析>>
科目: 来源: 题型:
【题目】某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com