
科目: 来源: 题型:
【题目】平行四边形的一条边长为6cm,那么这个平行四边形的两条对角线的长可以是( )
A. 8cm和3cm B. 8cm和4cm C. 8cm和5cm D. 8cm和20cm
查看答案和解析>>
科目: 来源: 题型:
【题目】已知如图,边长为2的正方形![]() 中,
中,![]() 是对角线
是对角线![]() 上的一个动点(与点
上的一个动点(与点![]() 、
、![]() 不重合),过点
不重合),过点![]() 作
作![]() ,
,![]() 交射线
交射线![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() .
.
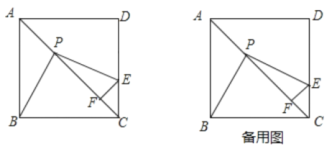
(1)求证:![]() :
:
(2)在点![]() 的运动过程中,
的运动过程中,![]() 的长度是否发生变化?若不变,试求出这个不变的值,写出解答过程:若变化,试说明理由:
的长度是否发生变化?若不变,试求出这个不变的值,写出解答过程:若变化,试说明理由:
(3)在点![]() 的运动过程中,
的运动过程中,![]() 能否为等腰三角形?如果能,直接写出此时
能否为等腰三角形?如果能,直接写出此时![]() 的长;如果不能,试说明理由.
的长;如果不能,试说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知△ABC中,AC=BC,以BC为直径的⊙O交AB于E,过点E作EG⊥AC于G,交BC的延长线于F.
(1)求证:FE是⊙O的切线;
(2)若FE=4,FC=2,求⊙O的半径及CG的长.
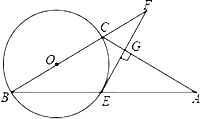
查看答案和解析>>
科目: 来源: 题型:
【题目】某校七年级(1)班班主任对本班学生进行了“我最喜欢的课外活动”的调查,并将调查结果分为书法和绘画类记为A;音乐类记为B;球类记为C;其他类记为D.根据调查结果发现该班每个学生都进行了等级且只登记了一种自己最喜欢的课外活动.班主任根据调查情况把学生都进行了归类,并制作了如下两幅统计图,请你结合图中所给信息解答下列问题:
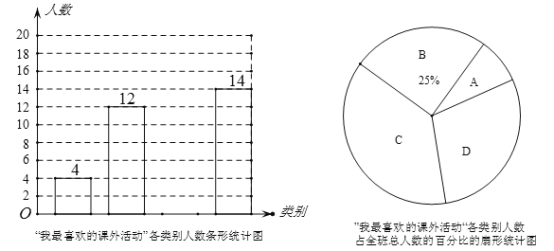
(1)七年级(1)班学生总人数为_______人,扇形统计图中D类所对应扇形的圆心角为_____度,请补全条形统计图;
(2)学校将举行书法和绘画比赛,每班需派两名学生参加,A类4名学生中有两名学生擅长书法,另两名擅长绘画.班主任现从A类4名学生中随机抽取两名学生参加比赛,请你用列表或画树状图的方法求出抽到的两名学生恰好是一名擅长书法,另一名擅长绘画的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】某垃圾处理厂,对不可回收垃圾的处理费用为90元/吨,可回收垃圾的分拣处理费用也为90元/吨,分拣后再被相关企业回收,回收价格如下表:
垃圾种类 | 纸类 | 塑料类 | 金属类 | 玻璃类 |
回收单价(元/吨) | 500 | 800 | 500 | 200 |
据了解,可回收垃圾占垃圾总量的60%,现有![]() 三个小区12月份产生的垃圾总量分别为100吨,100吨和
三个小区12月份产生的垃圾总量分别为100吨,100吨和![]() 吨.
吨.
(1)已知![]() 小区金属类垃圾质量是塑料类的5倍,纸类垃圾质量是塑料类的2倍.设塑料类的质量为
小区金属类垃圾质量是塑料类的5倍,纸类垃圾质量是塑料类的2倍.设塑料类的质量为![]() 吨,则
吨,则![]() 小区可回收垃圾有______吨,其中玻璃类垃圾有_____吨(用含
小区可回收垃圾有______吨,其中玻璃类垃圾有_____吨(用含![]() 的代数式表示)
的代数式表示)
(2)![]() 小区纸类与金属类垃圾总量为35吨,当月可回收垃圾回收总金额扣除所有垃圾处理费后,收益16500元.求12月份该小区可回收垃圾中塑料类垃圾的质量.
小区纸类与金属类垃圾总量为35吨,当月可回收垃圾回收总金额扣除所有垃圾处理费后,收益16500元.求12月份该小区可回收垃圾中塑料类垃圾的质量.
(3)![]() 小区发现塑料类与玻璃类垃圾的回收总额恰好相等,所有可回收垃圾的回收总金额为12000元.设该小区塑料类垃圾质量为
小区发现塑料类与玻璃类垃圾的回收总额恰好相等,所有可回收垃圾的回收总金额为12000元.设该小区塑料类垃圾质量为![]() 吨,求
吨,求![]() 与
与![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一个桌球游戏的长方形桌面![]() 中,
中,![]() ,现将球从
,现将球从![]() 边上的点
边上的点![]() 处发射,依次与边
处发射,依次与边![]() 触碰并反弹后第一次回到
触碰并反弹后第一次回到![]() 边上的点
边上的点![]() 处,设触碰点依次为
处,设触碰点依次为![]() ,当
,当![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 时,
时,![]() 等于________
等于________![]() .
.
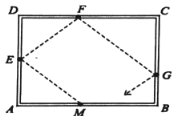
查看答案和解析>>
科目: 来源: 题型:
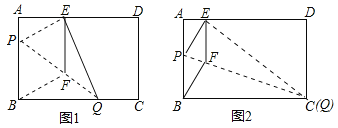
【题目】如图1,在矩形纸片![]() 中,
中,![]() ,
,![]() ,折叠纸片使点
,折叠纸片使点![]() 落在
落在![]() 上的点
上的点![]() 处,折痕为
处,折痕为![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .
.
(1)求证:四边形![]() 为菱形;
为菱形;
(2)当折痕![]() 的点
的点![]() 与点
与点![]() 重合时(如图2),求菱形
重合时(如图2),求菱形![]() 的边长.
的边长.
查看答案和解析>>
科目: 来源: 题型:
【题目】李老师准备购买若干个某种笔记本奖励学生,甲、乙两家商店都有足够数量的这种笔记本,其标价都是每个6元,甲商店的促销方案是:购买这种笔记本数量不超过5个时,原价销售;超过5个时,超过部分按原价的7折销售.乙商店的销售方案是:一律按标价的8折销售.
(1)若李老师要购买![]() 个这种笔记本,请用含
个这种笔记本,请用含![]() 的式子分别表示李老师到甲商店和乙商店购买全部这种笔记本所需的费用.
的式子分别表示李老师到甲商店和乙商店购买全部这种笔记本所需的费用.
(2)李老师购买多少个这种笔记本时,到甲、乙两家商店购买所需费用相同?
(3)若李老师需要20个这种笔记本,则到甲、乙哪家商店购买更优惠?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com