
科目: 来源: 题型:
【题目】阅读下面一段文字:
在数轴上点A,B分别表示数a,b.A,B两点间的距离可以用符号![]() 表示,利用有理数减法和绝对值可以计算A,B两点之间的距离
表示,利用有理数减法和绝对值可以计算A,B两点之间的距离![]() .
.
例如:当a=2,b=5时,![]() =5-2=3;当a=2,b=-5时,
=5-2=3;当a=2,b=-5时,![]() =
=![]() =7;当a=-2,b=-5时,
=7;当a=-2,b=-5时,![]() =
=![]() =3.综合上述过程,发现点A、B之间的距离
=3.综合上述过程,发现点A、B之间的距离![]() =
=![]() (也可以表示为
(也可以表示为![]() ).
).
请你根据上述材料,探究回答下列问题:
(1)数轴上表示1和3两点之间的距离是 ;
(2)表示数a和-2的两点间距离是6,则a= ;
(3)如果数轴上表示数a的点位于-4和3之间,求![]() 的值.
的值.
(4)是否存在数a,使代数式![]() 的值最小?若存在,请求出代数式的最小值,并直接写出数a的值或取值范围,若不存在,请简要说明理由.
的值最小?若存在,请求出代数式的最小值,并直接写出数a的值或取值范围,若不存在,请简要说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,过![]() 轴正半轴上的任意一点
轴正半轴上的任意一点![]() ,作
,作![]() 轴的平行线,分别与反比例函数
轴的平行线,分别与反比例函数![]() 和
和![]() 的图象交于点
的图象交于点![]() 和点
和点![]() ,点
,点![]() 是
是![]() 轴上一点,连接
轴上一点,连接![]() 、
、![]() ,则
,则![]() 的面积为( )
的面积为( )

A. 3B. 4C. 5D. 6
查看答案和解析>>
科目: 来源: 题型:
【题目】某商场准备进一批两种不同型号的衣服,已知购进A种型号衣服9件,B种型号衣服10件,则共需1810元;若购进A种型号衣服12件,B种型号衣服8件,共需1880元;已知销售一件A型号衣服可获利18元,销售一件B型号衣服可获利30元,要使在这次销售中获利不少于699元,且A型号衣服不多于28件.
(1)求A、B型号衣服进价各是多少元?
(2)若已知购进A型号衣服是B型号衣服的2倍还多4件,则商店在这次进货中可有几种方案并简述购货方案.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)已知∠ABC=90°,∠CBD=30°,BP平分∠ABD,请补全图形,并求∠ABP的度数.
(2)在(1)的条件下,若∠ABC=α,∠CBD=β,直接写出∠ABP的度数.
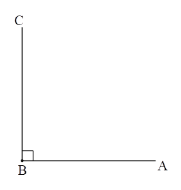
查看答案和解析>>
科目: 来源: 题型:
【题目】某校初一年级两个班的学生要到航天科普教育基地进行社会大课堂活动,其中初一(1)班有40多人,初一(2)班有50多人,教育基地门票价格如下:

原计划两班都以班为单位分别购票,则一共应付1106元.请回答下列问题:
(1)初一(2)班有多少人?
(2)你作为组织者如何购票最省钱?比原计划省多少钱?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在锐角△ABC中,∠ABC=45°,高线AD、BE相交于点F.
(1)判断BF与AC的数量关系并说明理由;
(2)如图2,将△ACD沿线段AD对折,点C落在BD上的点M,AM与BE相交于点N,当DE∥AM时,判断NE与AC的数量关系并说明理由.

【答案】(1)BF=AC,理由见解析;(2)NE=![]() AC,理由见解析.
AC,理由见解析.
【解析】试题分析:(1)如图1,证明△ADC≌△BDF(AAS),可得BF=AC;
(2)如图2,由折叠得:MD=DC,先根据三角形中位线的推论可得:AE=EC,由线段垂直平分线的性质得:AB=BC,则∠ABE=∠CBE,结合(1)得:△BDF≌△ADM,则∠DBF=∠MAD,最后证明∠ANE=∠NAE=45°,得AE=EN,所以EN=![]() AC.
AC.
试题解析:
(1)BF=AC,理由是:
如图1,∵AD⊥BC,BE⊥AC,
∴∠ADB=∠AEF=90°,
∵∠ABC=45°,
∴△ABD是等腰直角三角形,
∴AD=BD,
∵∠AFE=∠BFD,
∴∠DAC=∠EBC,
在△ADC和△BDF中,
∵ ,
,
∴△ADC≌△BDF(AAS),
∴BF=AC;
(2)NE=![]() AC,理由是:
AC,理由是:
如图2,由折叠得:MD=DC,
∵DE∥AM,
∴AE=EC,
∵BE⊥AC,
∴AB=BC,
∴∠ABE=∠CBE,
由(1)得:△ADC≌△BDF,
∵△ADC≌△ADM,
∴△BDF≌△ADM,
∴∠DBF=∠MAD,
∵∠DBA=∠BAD=45°,
∴∠DBA﹣∠DBF=∠BAD﹣∠MAD,
即∠ABE=∠BAN,
∵∠ANE=∠ABE+∠BAN=2∠ABE,
∠NAE=2∠NAD=2∠CBE,
∴∠ANE=∠NAE=45°,
∴AE=EN,
∴EN=![]() AC.
AC.
【题型】解答题
【结束】
19
【题目】某校学生会决定从三明学生会干事中选拔一名干事当学生会主席,对甲、乙、丙三名候选人进行了笔试和面试,三人的测试成绩如下表所示:
测试项目 | 测试成绩/分 | ||
甲 | 乙 | 丙 | |
笔试 | 75 | 80 | 90 |
面试 | 93 | 70 | 68 |
根据录用程序,学校组织200名学生采用投票推荐的方式,对三人进行民主测评,三人得票率如扇形统计图所示(没有弃权,每位同学只能推荐1人),每得1票记分.
(1)分别计算三人民主评议的得分;
(2)根据实际需要,学校将笔试、面试、民主评议三项得分按3:3:4的比例确定个人成绩,三人中谁会当选学生会主席?

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,![]() ,
,![]() 平分
平分![]() ,与
,与![]() 边交于点
边交于点![]() ,
,![]() 平分
平分![]() ,与
,与![]() 边交于点
边交于点![]() .
.
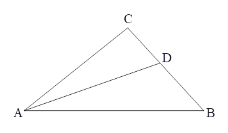
(1)依题意补全图形,并猜想![]() 的度数等于 ;
的度数等于 ;
(2)填空,补全下面的证明过程.
∵ ![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,
∴ ![]() ,
,![]() .(理由: )
.(理由: )
∵![]() ,
,
∴![]() ______
______![]() _________
_________![]() _________
_________![]() _____
_____![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】某村庄计划建造A,B两种型号的沼气池共20个,以解决该村所有农户的燃料问题.两种型号沼气池的占地面积和可供使用农户数见下表:
型号 | 占地面积 (单位:m2/个) | 可供使用农户数 (单位:户/个) |
A | 15 | 18 |
B | 20 | 30 |
已知可供建造沼气池的占地面积不超过365m2,该村农户共有492户.
(1)如何合理分配建造A,B型号“沼气池”的个数才能满足条件?满足条件的方案有几种?通过计算分别写出各种方案.
(2)请写出建造A、B两种型号的“沼气池”的总费用y和建造A型“沼气池”个数x之间的函数关系式;
(3)若A型号“沼气池”每个造价2万元,B型号“沼气池”每个造价3万元,试说明在(1)中的各种建造方案中,哪种建造方案最省钱,最少的费用需要多少万元?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在锐角△ABC中,∠ABC=45°,高线AD、BE相交于点F.
(1)判断BF与AC的数量关系并说明理由;
(2)如图2,将△ACD沿线段AD对折,点C落在BD上的点M,AM与BE相交于点N,当DE∥AM时,判断NE与AC的数量关系并说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,表中给出的是某月的月历,任意选取“U”型框中的7个数(如阴影部分所示),请你运用所学的数学知识来研究,发现这7个数的和不可能的是( )
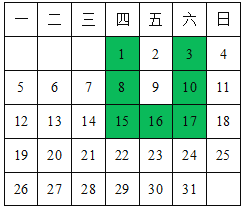
A.70B.78C.84D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com