
科目: 来源: 题型:
【题目】如图,P是矩形ABCD内的任意一点,连接PA、PB、PC、PD,得到△PAB、△PBC、△PCD、△PDA,设它们的面积分别是S1、S2、S3、S4,给出如下结论:
①S1+S2=S3+S4② S2+S4= S1+ S3
③若S3=2S1,则S4=2S2④若S1= S2,则P点在矩形的对角线上
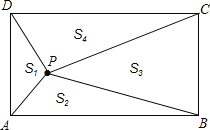
其中正确的结论的序号是 ▲ (把所有正确结论的序号都填在横线上).
查看答案和解析>>
科目: 来源: 题型:
【题目】某中学对本校500名毕业生中考体育加试测试情况进行调查,根据男生1 000m及女生800m测试成绩整理、绘制成如下不完整的统计图(图①、图②),请根据统计图提供的信息,回答下列问题:
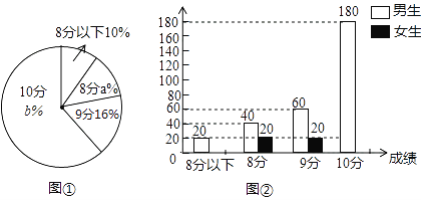
(1)该校毕业生中男生有________人,女生有________人;
(2)扇形统计图中a=________,b=________;
(3)补全条形统计图(不必写出计算过程).
查看答案和解析>>
科目: 来源: 题型:
【题目】父亲带着两个儿子向离家33千米的奶奶家出发,父亲有一辆摩托车,速度为25千米![]() 小时,如果再载了另一个人,则速度为20千米
小时,如果再载了另一个人,则速度为20千米![]() 小时
小时![]() 摩托车不允许带两个人,即每车至多载两人
摩托车不允许带两个人,即每车至多载两人![]() 每个儿子如果步行速度为5千米
每个儿子如果步行速度为5千米![]() 小时,为尽快到达奶奶家,出发时,父亲让第二个儿子先步行,将第一个儿子载了一段路程后让其步行前往奶奶家,并立即返回接步行的第二个儿子,结果与第一个儿子同时到达奶奶家,则在路上共计用的时间为______小时.
小时,为尽快到达奶奶家,出发时,父亲让第二个儿子先步行,将第一个儿子载了一段路程后让其步行前往奶奶家,并立即返回接步行的第二个儿子,结果与第一个儿子同时到达奶奶家,则在路上共计用的时间为______小时.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平行四边形ABCD中,E,F分别是边AD,BC的中点,AC分别交BE,DF于点M,N,给出下列结论:①△ABM≌△CDN;②AM=![]() AC;③DN=2NF;④S△AMB=
AC;③DN=2NF;④S△AMB=![]() S△ABC,其中正确的结论是__ __.(填序号)
S△ABC,其中正确的结论是__ __.(填序号)
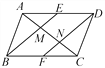
查看答案和解析>>
科目: 来源: 题型:
【题目】梯形ABCD中AB∥CD,∠ADC+∠BCD=90°,以AD、AB、BC为斜边向形外作等腰直角三角形,其面积分别是![]() ,且
,且![]() ,则CD=( )
,则CD=( )

A.2.5ABB.3ABC.3.5ABD.4AB
查看答案和解析>>
科目: 来源: 题型:
【题目】已知在直角梯形ABCD中, AD∥BC,∠BCD=90°, BC=CD=2AD , E、F分别是BC、CD边的中点,连结BF、DE交于点P,连结CP并延长交AB于点Q,连结AF,则下列结论不正确的是( )
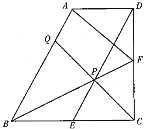
A.CP 平分∠BCDB.四边形 ABED 为平行四边形
C.CQ将直角梯形 ABCD 分为面积相等的两部分D.△ABF为等腰三角形
查看答案和解析>>
科目: 来源: 题型:
【题目】一个不透明的布袋里装有3个球,其中2个红球,1个白球,它们除颜色外其余都相同.
(1)求摸出1个球是白球的概率;
(2)摸出1个球,记下颜色后放回,并搅匀,再摸出1个球,求两次摸出的球恰好颜色不同的概率(要求画树状图或列表);
(3)现再将n个白球放入布袋,搅匀后,使摸出1个球是白球的概率为![]() ,求n的值.
,求n的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】下表记录了一名球员在罚球线上投篮的结果.
投篮次数(n) | 50 | 100 | 150 | 200 | 250 | 300 | 350 |
投中次数(m) | 28 | 60 | 78 | 104 | 123 | 152 | 251 |
投中频率( |
|
|
|
|
|
|
|
(1)计算表中的投中频率(精确到0.01);
(2)这名球员投篮一次,投中的概率约是多少(精确到0.1)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com