
科目: 来源: 题型:
【题目】探究问题:
(1)方法感悟:
如图①,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足∠BAF=45°,连接EF,求证DE+BF=EF.感悟解题方法,并完成下列填空:将△ADE绕点A顺时针旋转90°得到△ABG,此时AB与AD重合,由旋转可得:AB=AD,BG=DE,∠1=∠2,∠ABG=∠D=90°,∴ ∠ABG+∠ABF=90°+90°=180°,因此,点G,B,F在同一条直线上.
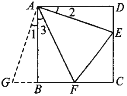
∵ ∠EAF=45°∴ ∠2+∠3=∠BAD-∠EAF=90°-45°=45°.
∵ ∠1=∠2,∠1+∠3=45°.
即∠GAF=∠________.
又AG=AE,AF=AE
∴ △GAF≌△________.
∴ _________=EF,故DE+BF=EF.
(2)方法迁移:
如图②,将Rt△ABC沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF=![]() ∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想.
∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想.
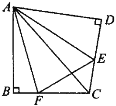
查看答案和解析>>
科目: 来源: 题型:
【题目】观察下面三行数:
2,﹣4,8,﹣16,32,﹣64,…
4,﹣2,10,﹣14,34,﹣62,…
﹣1,2,﹣4,8,﹣16,32,…
在上面三行数的第n列中,从上往下的三个数分别记为a,b,c,观察这些数的特点,根据你所得到的规律,解答下列为问题.
(1)用含n的式子分别表示出a,b,c;
(2)根据(1)的结论,若a,b,c三个数的和为770,求n的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】一些数学问题的研究可以经历观察、探究、发现、证明等过程.下面是对一个问题的部分研究过程:
(观察)![]() =
=![]() ,
,![]() =
=![]() ,
,![]() 是否也能写成分数的形式?
是否也能写成分数的形式?
(探究1)设![]() =x,
=x,
由![]() =0.555…可知,10x=5.555…,
=0.555…可知,10x=5.555…,
所以10x﹣x=5.
解方程,得x=![]()
于是,得![]() =
=![]() .
.
所以,![]() 能写成分数的形式
能写成分数的形式
(探究2)仿照上面的方法,尝试将![]() 写成分数的形式.
写成分数的形式.
(发现) .
请你完成(探究2)的部分,并用一句话概括你的发现
查看答案和解析>>
科目: 来源: 题型:
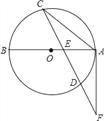
【题目】如图,已知AB是⊙O的直径,弦CD与AB交于点E,F为CD的延长线上一点,连接AF,且FA2=FDFC.
(1)求证:FA为⊙O的切线;
(2)若AC=8,CE:ED=6:5,AE:EB=2:3,求AB的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如果两个角之差的绝对值等于45°,则称这两个角互为“半余角”,即若|∠α-∠β |=45°,则称∠α、∠β互为半余角.(注:本题中的角是指大于0°且小于180°的角)
(1)若∠A=80°,则∠A的半余角的度数为 ;
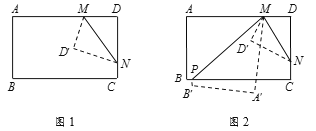
(2)如图1,将一长方形纸片ABCD沿着MN折叠(点M在线段AD上,点N在线段CD上)使点D落在点D′处,若∠AMD′与∠DMN互为“半余角”,求∠DMN的度数;
(3)在(2)的条件下,再将纸片沿着PM折叠(点P在线段BC上),点A、B分别落在点A′、B′处,如图2.若∠AMP比∠DMN大5°,求∠A′MD′的度数.
查看答案和解析>>
科目: 来源: 题型:
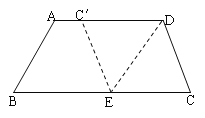
【题目】如图,在梯形纸片ABCD中,AD∥BC,AD>CD,将纸片沿过点D的直线折叠,使点C落在AD上的点C′处,折痕DE交BC于点E,连结C′E.
(1)求证:四边形ECDC′是菱形;
(2)若BC=CD+AD,试判断四边形ABED的形状,并加以证明.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两车都从A地出发,在路程为360千米的同一道路上驶向B地.甲车先出发匀速驶向B地.10分钟后乙车出发,乙车匀速行驶3小时后在途中的配货站装货耗时20分钟.由于满载货物,乙车速度较之前减少了40千米/时.乙车在整个途中共耗时![]() 小时,结果与甲车同时到达B地.
小时,结果与甲车同时到达B地.
(1)甲车的速度为 千米/时;
(2)求乙车装货后行驶的速度;
(3)乙车出发 小时与甲车相距10千米?
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两支“徒步队”到野外沿相同路线徒步,徒步的路程为24千米.甲队步行速度为4千米/时,乙队步行速度为6千米/时.甲队出发1小时后,乙队才出发,同时乙队派一名联络员跑步在两队之间来回进行一次联络(不停顿),他跑步的速度为10千米/时.
(1)乙队追上甲队需要多长时间?
(2)联络员从出发到与甲队联系上后返回乙队时,他跑步的总路程是多少?
(3)从甲队出发开始到乙队完成徒步路程时止,何时两队间间隔的路程为1千米?
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面内,将一副直角三角板按如图所示的方式摆放,其中三角形ABC为含60°角的直角三角板,三角形BDE为含45°角的直角三角板.

(1)如图1,若点D在AB上,则∠EBC的度数为 ;
(2)如图2,若∠EBC=170°,则∠α的度数为 ;
(3)如图3,若∠EBC=118°,求∠α的度数;
(4)如图3,若0°<∠α<60°,求∠ABE-∠DBC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com