
科目: 来源: 题型:
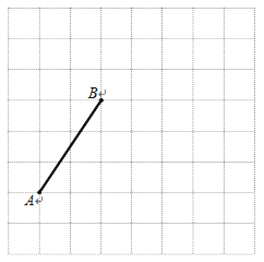
【题目】下图是由边长为1个单位长度的小正方形组成的网格,线段AB的端点在格点上.
(1)请建立适当的平面直角坐标系xOy,使得A点的坐标为(-3,-1),在此坐标系下,B点的坐标为________________;
(2)将线段BA绕点B逆时针旋转90°得线段BC,画出BC;在第(1)题的坐标系下,C点的坐标为__________________;
(3)在第(1)题的坐标系下,二次函数y=ax2+bx+c(a≠0)的图象过O、B、C三点,则此函数图象的对称轴方程是________________.
【答案】 (-1,2) (2,0) x=1
【解析】分析:![]() 根据点
根据点![]() 的坐标建立坐标系,即可写出点
的坐标建立坐标系,即可写出点![]() 的坐标.
的坐标.
![]() 画出点
画出点![]() 旋转后的对应点
旋转后的对应点![]() 连接
连接![]() ,写出点
,写出点![]() 的坐标.
的坐标.
![]() 用待定系数法求出函数解析式,即可求出对称轴方程.
用待定系数法求出函数解析式,即可求出对称轴方程.
详解:(1)建立坐标系如图,
B点的坐标为![]() ;
;
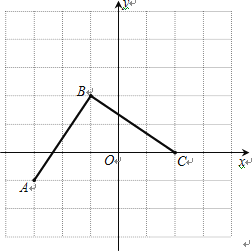
(2)线段BC如图,C点的坐标为![]()
(3)把点![]() 代入二次函数
代入二次函数![]() ,得
,得
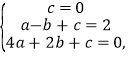
解得: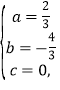
二次函数解析为:![]()
对称轴方程为:![]()
故对称轴方程是![]()
点睛:考查图形与坐标;旋转、对称变换;待定系数法求二次函数解析式,二次函数的图象与性质.熟练掌握各个知识点是解题的关键.
【题型】解答题
【结束】
18
【题目】特殊两位数乘法的速算——如果两个两位数的十位数字相同,个位数字相加为10,那么能立说出这两个两位数的乘积.如果这两个两位数分别写作AB和AC(即十位数字为A,个位数字分别为B、C,B+C=10,A>3),那么它们的乘积是一个4位数,前两位数字是A和(A+1)的乘积,后两位数字就是B和C的乘积.
如:47×43=2021,61×69=4209.
(1)请你直接写出83×87的值;
(2)设这两个两位数的十位数字为x(x>3),个位数字分别为y和z(y+z=10),通过计算验证这两个两位数的乘积为100x(x+1)+yz.
(3)99991×99999=___________________(直接填结果)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,∠AOB=60°,OA=OB,动点C从点O出发,沿射线OB方向移动,以AC为边在右侧作等边△ACD,连接BD,则BD所在直线与OA所在直线的位置关系是( )
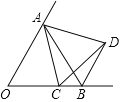
A. 平行 B. 相交 C. 垂直 D. 平行、相交或垂直
查看答案和解析>>
科目: 来源: 题型:
【题目】特殊两位数乘法的速算——如果两个两位数的十位数字相同,个位数字相加为10,那么能立说出这两个两位数的乘积.如果这两个两位数分别写作AB和AC(即十位数字为A,个位数字分别为B、C,B+C=10,A>3),那么它们的乘积是一个4位数,前两位数字是A和(A+1)的乘积,后两位数字就是B和C的乘积.
如:47×43=2021,61×69=4209.
(1)请你直接写出83×87的值;
(2)设这两个两位数的十位数字为x(x>3),个位数字分别为y和z(y+z=10),通过计算验证这两个两位数的乘积为100x(x+1)+yz.
(3)99991×99999=___________________(直接填结果)
【答案】7221
【解析】分析:![]() 套用上面的归纳总结代入数据,即可得出结论;
套用上面的归纳总结代入数据,即可得出结论;
![]() 利用上面总结的结论套入数据表示出该两个两位数的成绩,在将等式展开合并同类项得出左边=右边,从而证明结论成立.
利用上面总结的结论套入数据表示出该两个两位数的成绩,在将等式展开合并同类项得出左边=右边,从而证明结论成立.
![]() 直接运算即可.
直接运算即可.
详解:(1)83和87满足题中的条件,即十位数都是8,8>3,且个位数字分别是3和7,之和为10,那么它们的乘积是一个4位数,前两位数字是8和9的乘积,后两位数字就是3和7的乘积,因而,答案为:7221.
(2) 这两个两位数的十位数字为x(x>3),个位数字分别为y和z,则由题知y+z=10,
因而有:(10x+y)(10x+z)=100x2+10xz+10xy+yz
=100x2+10x(y+z)+yz,
=100x2+100x+yz,
=100x(x+1)+yz.
(3)9999000009.
点睛:通过阅读题干掌握题中所给信息得出推理方法,然后通过多项式的展开式得出答案.学生应熟练掌握归纳推理的数学思想.
【题型】解答题
【结束】
19
【题目】为了大力弘扬和践行社会主义核心价值观,某乡镇在一条公路旁的小山坡上,树立一块大型标语牌AB,如图所示,标语牌底部B点到山脚C点的距离BC为20米,山坡的坡角为30°. 某同学在山脚的平地F处测量该标语牌的高,测得点C到测角仪EF的水平距离CF = 1.7米,同时测得标语牌顶部A点的仰角为45°,底部B点的仰角为20°,求标语牌AB的高度.(参考数值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,![]() )
)
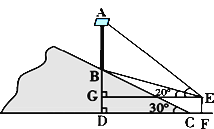
查看答案和解析>>
科目: 来源: 题型:
【题目】为了大力弘扬和践行社会主义核心价值观,某乡镇在一条公路旁的小山坡上,树立一块大型标语牌AB,如图所示,标语牌底部B点到山脚C点的距离BC为20米,山坡的坡角为30°. 某同学在山脚的平地F处测量该标语牌的高,测得点C到测角仪EF的水平距离CF = 1.7米,同时测得标语牌顶部A点的仰角为45°,底部B点的仰角为20°,求标语牌AB的高度.(参考数值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,![]() )
)
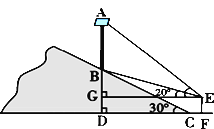
【答案】标语牌AB的高度约为12.16米.
【解析】分析:![]() 解直角三角形求处CD的长度,则
解直角三角形求处CD的长度,则![]() 然后在直角
然后在直角![]() 中即可求得
中即可求得![]() 的长,在Rt△AGE中,求得
的长,在Rt△AGE中,求得![]() 的长,从而求得
的长,从而求得![]() 的高度..
的高度..
详解:在Rt△BDC中,![]() BC = 20米,
BC = 20米,![]()
∴![]()
∴![]()
∴![]()
在Rt△BGE中,![]()
∴![]()
在Rt△AGE中,![]()
∴![]()
∴![]()
答:标语牌AB的高度约为12.16米.
点睛:考查解直角三角形的应用,结合图形利用三角函数解三角形即可.
【题型】解答题
【结束】
20
【题目】已知AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点D(如图1).
(1)若AB=2,∠B=30°,求CD的长;
(2) 取AC的中点E,连结D、E(如图2),求证:DE与⊙O相切.
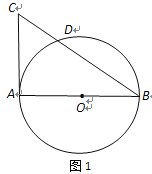
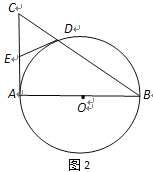
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点C是直线AB,DE之间的一点,∠ACD=90°,下列条件能使得AB∥DE的是( )
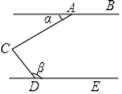
A. ∠α+∠β=180° B. ∠β﹣∠α=90° C. ∠β=3∠α D. ∠α+∠β=90°
查看答案和解析>>
科目: 来源: 题型:
【题目】已知AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点D(如图1).
(1)若AB=2,∠B=30°,求CD的长;
(2) 取AC的中点E,连结D、E(如图2),求证:DE与⊙O相切.

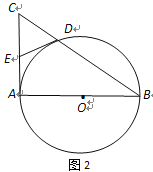
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】分析:![]() 连接AD ,根据AC是⊙O的切线,AB是⊙O的直径,得到∠CAB=∠ADB=90°,根据∠B=30°,解直角三角形求得
连接AD ,根据AC是⊙O的切线,AB是⊙O的直径,得到∠CAB=∠ADB=90°,根据∠B=30°,解直角三角形求得![]() 的长度.
的长度.
![]() 连接OD,AD.根据DE=CE=EA,∠EDA=∠EAD. 根据OD=OA,得到
连接OD,AD.根据DE=CE=EA,∠EDA=∠EAD. 根据OD=OA,得到
∠ODA=∠DAO,得到∠EDA+∠ODA=∠EAD+∠DAO.得到∠EDO=90°即可.
详解:(1)如图,连接AD ,
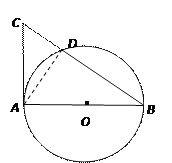
∵AC是⊙O的切线,AB是⊙O的直径,
∴∠CAB=∠ADB=90°,
∴ΔCAB,ΔCAD均是直角三角形.
∴∠CAD=∠B=30°.
在RtΔCAB中,AC=ABtan30°=![]()
∴在RtΔCAD中,CD=ACsin30°=![]()
(2)如图,连接OD,AD.

∵AC是⊙O的切线,AB是⊙O的直径,
∴∠CAB=∠ADB=∠ADC=90°,
又∵E为AC中点,
∴DE=CE=EA,
∴∠EDA=∠EAD.
∵OD=OA,
∴∠ODA=∠DAO,
∴∠EDA+∠ODA=∠EAD+∠DAO.
即:∠EDO=∠EAO=90°.
又点D在⊙O上,因此DE与⊙O相切.
点睛:考查解直角三角形,圆周角定理,切线的判定与性质等,属于圆的综合题,比较基础.注意切线的证明方法,是高频考点.
【题型】解答题
【结束】
21
【题目】课外活动时间,甲、乙、丙、丁4名同学相约进行羽毛球比赛.
(1)如果将4名同学随机分成两组进行对打,求恰好选中甲乙两人对打的概率;
(2)如果确定由丁担任裁判,用“手心、手背”的方法在另三人中竞选两人进行比赛.竞选规则是:三人同时伸出“手心”或“手背”中的一种手势,如果恰好只有两人伸出的手势相同,那么这两人上场,否则重新竞选.这三人伸出“手心”或“手背”都是随机的,求一次竞选就能确定甲、乙进行比赛的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】某同学在![]() ,
,![]() 两家超市发现他看中的随身听的单价相同,书包单价也相同,随身听和书包单价之和是
两家超市发现他看中的随身听的单价相同,书包单价也相同,随身听和书包单价之和是![]() 元,且随身听的单价比书包的单价的
元,且随身听的单价比书包的单价的![]() 倍少
倍少![]() 元.
元.
(1)求该同学看中的随身听和书包的单价各是多少元?
(2)某一天该同学上街,恰好赶上商家促销,超市![]() 所有商品打八五折销售,超市
所有商品打八五折销售,超市![]() 全场购物每满
全场购物每满![]() 元返购物券
元返购物券![]() 元销售(不足
元销售(不足![]() 元不返券,购物券全场通用),但他只带了
元不返券,购物券全场通用),但他只带了![]() 元钱,如果他只在一家超市购买看中的这两样商品,你能说明他可以选择哪一家购买吗?若两家都可以选择,在哪一家购买更省钱?
元钱,如果他只在一家超市购买看中的这两样商品,你能说明他可以选择哪一家购买吗?若两家都可以选择,在哪一家购买更省钱?
查看答案和解析>>
科目: 来源: 题型:
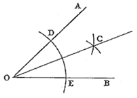
【题目】如图,已知![]() ,小明按如下步骤作图:
,小明按如下步骤作图:
(1)以点O为圆心,适当长为半径画弧,交OA于D,交OB于点E
(2)分别以点D、E为圆心,大于![]() 的长为半径画弧,两弧在
的长为半径画弧,两弧在![]() 的内部相交于点C
的内部相交于点C
(3)画射线OC
根据上述作图步骤,下列结论正确的有( )个
①射线OC是![]() 的平分线;②点O和点C关于直线DE对称;③射线OC垂直平分线段DE;④
的平分线;②点O和点C关于直线DE对称;③射线OC垂直平分线段DE;④![]() .
.
A.1B.2C.3D.4
查看答案和解析>>
科目: 来源: 题型:
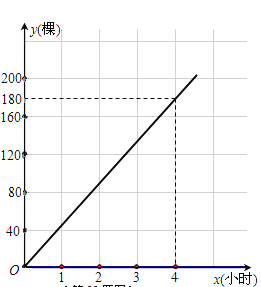
【题目】为了“绿化环境,美化家园”,3月12日(植树节)上午8点,某校901、902班同学同时参加义务植树.901班同学始终以同一速度种植树苗,种植树苗的棵数y1与种植时间x(小时)的函数图象如图所示;902班同学开始以1小时种植40棵的速度工作了1.5小时后,因需更换工具而停下休息半小时,更换工具后种植速度提高至原来的1.5倍.
(1)求902班同学上午11点时种植的树苗棵数;
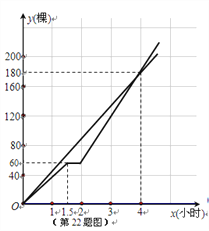
(2)分别求出901班种植数量y1、902班种植数量y2与种植时间x(小时)之间的函数关系式,并在所给坐标系上画出y2关于x的函数图象;
(3)已知购买树苗不多于120棵时,每棵树苗的价格是20元;购买树苗超过120棵时,超过的部分每棵价格17元.若本次植树所购树苗的平均成本是18元,则两班同学上午几点可以共同完成本次植树任务?
【答案】(1)120棵;(2)见解析;(3)两班同学上午12点可以共同完成本次植树任务.
【解析】分析:![]() 直接进行计算即可.
直接进行计算即可.
![]() 用待定系数法求一次函数解析式即可, 902班的要分成3段.
用待定系数法求一次函数解析式即可, 902班的要分成3段.
![]() 当x=2时,两班同学共植树150棵,
当x=2时,两班同学共植树150棵,![]() 平均成本:不符合题意;,x>2,两班共植树(105x-60)棵.列出方程
平均成本:不符合题意;,x>2,两班共植树(105x-60)棵.列出方程![]() 求解即可.
求解即可.
详解:(1)902班同学上午11点时种植的树苗棵数为:
![]() (棵)
(棵)
(2)由图可知,y1是关于x的正比例函数,可设y1=k1x,经过(4,180),
代入可得![]()
∴![]() (x≥0),
(x≥0),
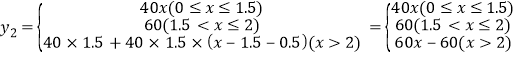 ,
,
y2关于x的函数图象如图所示.
(3)当x=2时,两班同学共植树150棵,
![]() 平均成本:
平均成本:
所以,x>2,两班共植树(105x-60)棵.
![]() 由题意可得:
由题意可得:
解得:x=4.
![]() ,
,
所以,两班同学上午12点可以共同完成本次植树任务.
点睛:考查了待定系数法求一次函数解析式,一元一次方程的应用,注意分类讨论
的数学思想方法.
【题型】解答题
【结束】
23
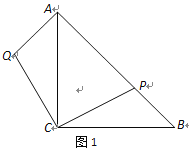
【题目】在等腰直角△ABC中,,AC=BC,点P在斜边AB上(AP>BP).作AQ⊥AB,且AQ=BP,连结CQ(如图1).
(1)求证:△ACQ≌△BCP;
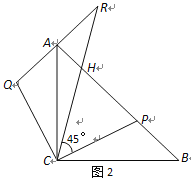
(2)延长QA至点R,使得∠RCP=45°,RC与AB交于点H,如图2.
①求证:CQ2=QA·QR ;
②判断三条线段AH、HP、PB的长度满足的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com