
科目: 来源: 题型:
【题目】某单位计划在暑假阴间组织员工到某地旅游,参加旅游的人数估计为10~25人,甲、乙两家旅行社的服务质量相同,且报价都是每人200元.经过协商,甲旅行社表示可给予每位游客七折优惠;乙旅行社表示可先免去一位游客的费用,其余游客七五折优惠.设该单位参加旅游的人数是x人.选择甲旅行社时,所需费用为![]() 元,选择乙旅行社时,所需费用为
元,选择乙旅行社时,所需费用为![]() 元.
元.
(1)写出甲旅行社收费![]() (元)与参加旅游的人数x(人)之间的关系式.
(元)与参加旅游的人数x(人)之间的关系式.
(2)写出乙旅行社收费![]() (元)与参加旅游的人数x(人)之间的关系式.
(元)与参加旅游的人数x(人)之间的关系式.
(3)该单位选择哪一家旅行社支付的旅游费用较少?
查看答案和解析>>
科目: 来源: 题型:
【题目】在综合与实践课上,老师请同学们以“两条平行线![]() ,
,![]() 和一块含
和一块含![]() 角的直角三角尺
角的直角三角尺![]() (
(![]() ,
,![]() )”为主题开展数学活动.
)”为主题开展数学活动.
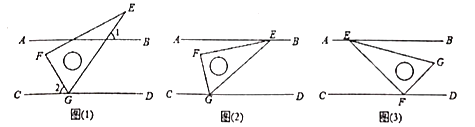
(1)如图(1),把三角尺的![]() 角的顶点
角的顶点![]() 放在
放在![]() 上,若
上,若![]() ,求
,求![]() 的度数;
的度数;
(2)如图(2),小颖把三角尺的两个锐角的顶点![]() 、
、![]() 分别放在
分别放在![]() 和
和![]() 上,请你探索并说明
上,请你探索并说明![]() 与
与![]() 之间的数量关系;
之间的数量关系;
(3)如图(3),小亮把三角尺的直角顶点![]() 放在
放在![]() 上,
上,![]() 角的顶点
角的顶点![]() 落在
落在![]() 上.若
上.若![]() ,
,![]() ,请用含
,请用含![]() ,
,![]() 的式子直接表示
的式子直接表示![]() 与
与![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数![]() (m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.
(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.
(1)求该反比例函数和一次函数的解析式;
(2)求点B的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】知识链接:
“转化、化归思想”是数学学习中常用的一种探究新知、解决问题的基本的数学思想方法,通过“转化、化归”通常可以实现化未知为已知,化复杂为简单,从而使问题得以解决.
(1)问题背景:已知:△ABC.试说明:∠A+∠B+∠C=180°.
问题解决:(填出依据)
解:(1)如图①,延长AB到E,过点B作BF∥AC.
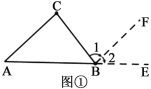
∵BF∥AC(作图)
∴∠1=∠C( )
∠2=∠A( )
∵∠2+∠ABC+∠1=180°(平角的定义)
∴∠A+∠ABC+∠C=180°(等量代换)
小结反思:本题通过添加适当的辅助线,把三角形的三个角之和转化成了一个平角,利用平角的定义,说明了数学上的一个重要结论“三角形的三个内角和等于180°.”
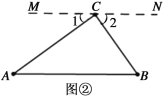
(2)类比探究:请同学们参考图②,模仿(1)的解决过程试说明“三角形的三个内角和等于180°”
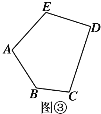
(3)拓展探究:如图③,是一个五边形,请直接写出五边形ABCDE的五个内角之和∠A+∠B+∠C+∠D+∠E= .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在直角坐标平面上,△AOB是直角三角形,点O在原点上,A、B两点的坐标分别为(-1,y1)、(3,y2),线段AB交y轴于点C.若S△AOC=1,记∠AOC为α,∠BOC为β,则sin α·sin β的值为____.

查看答案和解析>>
科目: 来源: 题型:
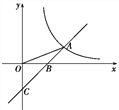
【题目】如图,已知直线y=x-2与y轴交于点C,与x轴交于点B,与反比例函数y=![]() 的图象在第一象限交于点A,连接OA,若S△AOB∶S△BOC=1∶2,则k的值为____.
的图象在第一象限交于点A,连接OA,若S△AOB∶S△BOC=1∶2,则k的值为____.
查看答案和解析>>
科目: 来源: 题型:
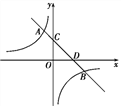
【题目】如图,反比例函数y=![]() 与一次函数y=k2x-k2+2在同一直角坐标系中的图象相交于A,B两点,其中A(-1,3),直线y=k2x-k2+2与坐标轴分别交于C,D两点,下列说法:①k1,k2<0;②点B的坐标为(3,-1);③当x<-1时,
与一次函数y=k2x-k2+2在同一直角坐标系中的图象相交于A,B两点,其中A(-1,3),直线y=k2x-k2+2与坐标轴分别交于C,D两点,下列说法:①k1,k2<0;②点B的坐标为(3,-1);③当x<-1时,![]() <k2x-k2+2;④tan∠OCD=-
<k2x-k2+2;④tan∠OCD=-![]() ,其中正确的是( )
,其中正确的是( )
A. ①③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
科目: 来源: 题型:
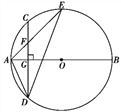
【题目】如图,AB是☉O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足![]() =
=![]() ,连接AF并延长交☉O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论:①△ADF∽△AED;②FG=3;③tan∠E=
,连接AF并延长交☉O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论:①△ADF∽△AED;②FG=3;③tan∠E=![]() ;④S△ADF=6
;④S△ADF=6![]() .
.
其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目: 来源: 题型:
【题目】学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:
碟子的个数 | 碟子的高度(单位:cm) |
1 | 2 |
2 | 2+1.5 |
3 | 2+3 |
4 | 2+4.5 |
… | … |

(1)当桌子上放有x(个)碟子时,请写出此时碟子的高度(用含x的式子表示);
(2)分别从三个方向上看,其三视图如上图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com