
科目: 来源: 题型:
【题目】如图,等边△ABC的边长为6,点O是三边垂直平分线的交点,∠FOG=120°,∠FOG的两边OF,OG分别交AB,BC与点D,E,∠FOG绕点O顺时针旋转时,下列四个结论正确的是( )

①OD=OE;②![]() ;③
;③![]() ;④△BDE的周长最小值为9,
;④△BDE的周长最小值为9,
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目: 来源: 题型:
【题目】中国“一带一路”战略给沿线国家和地区带来很大的经济效益,沿线某地区居民2015年年收入200美元,预计2017年年收入将达到1000美元,设2015年到2017年该地区居民年人均收入平均增长率为x,可列方程为![]()
![]()
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】甲乙两地相距180km,一列慢车以40km/h的速度从甲地匀速驶往乙地,慢车出发30分钟后,一列快车以60km/h的速度从甲地匀速驶往乙地.两车相继到达终点乙地,再次过程中,两车恰好相距10km的次数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,矩形ABCD的顶点A在x轴的正半轴上,顶点D在y轴的正半轴上,点B、点C在第一象限,sin∠OAD=![]() ,线段AD、AB的长分别是方程x2﹣11x+24=0的两根(AD>AB).
,线段AD、AB的长分别是方程x2﹣11x+24=0的两根(AD>AB).
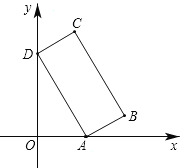
(1)求点B的坐标;
(2)求直线AB的解析式;
(3)在直线AB上是否存在点M,使以点C、点B、点M为顶点的三角形与△OAD相似?若存在,请直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两城相距800千米,一辆客车从甲城开往乙城,车速为![]() 千米
千米![]() 小时,同时一辆出租车从乙城开往甲城,车速为90千米
小时,同时一辆出租车从乙城开往甲城,车速为90千米![]() 小时,设客车行驶时间为
小时,设客车行驶时间为![]() 小时
小时![]()
![]() 当
当![]() 时,客车与乙城的距离为多少千米
时,客车与乙城的距离为多少千米![]() 用含a的代数式表示
用含a的代数式表示![]()
![]() 已知
已知![]() ,丙城在甲、乙两城之间,且与甲城相距260千米
,丙城在甲、乙两城之间,且与甲城相距260千米
![]() 求客车与出租车相距100千米时客车的行驶时间;
求客车与出租车相距100千米时客车的行驶时间;![]() 列方程解答
列方程解答![]()
![]() 已知客车和出租车在甲、乙之间的服务站M处相遇时,出租车乘客小王突然接到开会通知,需要立即返回,此时小王有两种返回乙城的方案:
已知客车和出租车在甲、乙之间的服务站M处相遇时,出租车乘客小王突然接到开会通知,需要立即返回,此时小王有两种返回乙城的方案:
方案一:继续乘坐出租车到丙城,加油后立刻返回乙城,出租车加油时间忽略不计;
方案二:在M处换乘客车返回乙城.
试通过计算,分析小王选择哪种方案能更快到达乙城?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1是一个有两个圆柱形构成的容器,最下面的圆柱形底面半径![]() 。匀速地向空容器内注水,水面高度
。匀速地向空容器内注水,水面高度![]() (单位:米)与时间
(单位:米)与时间![]() (单位:小时)的关系如图2所示。
(单位:小时)的关系如图2所示。

(1)求水面高度![]() 与时间
与时间![]() 的函数关系式;
的函数关系式;
(2)求注水的速度(单位:立方米/每小时),并求容器内水的体积![]() 与注水时间
与注水时间![]() 的函数关系式;
的函数关系式;
(3)求上面圆柱的底面半径(壁厚忽略不计)。
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下面材料:
小明在数学课外小组活动时遇到这样一个问题:
如果一个不等式(含有不等号的式子)中含有绝对值,并且绝对值符号中含有未知数,我们把这个不等式叫做绝对值不等式.
求绝对值不等式![]() 的解集(满足不等式的所有解).
的解集(满足不等式的所有解).
小明同学的思路如下:
先根据绝对值的定义,求出![]() 恰好是3时
恰好是3时![]() 的值,并在数轴上表示为点
的值,并在数轴上表示为点![]() ,
,![]() ,如图所示.观察数轴发现,
,如图所示.观察数轴发现,
![]()
以点![]() ,
,![]() 为分界点把数轴分为三部分:
为分界点把数轴分为三部分:
点![]() 左边的点表示的数的绝对值大于3;
左边的点表示的数的绝对值大于3;
点![]() ,
,![]() 之间的点表示的数的绝对值小于3;
之间的点表示的数的绝对值小于3;
点B右边的点表示的数的绝对值大于3.
因此,小明得出结论,绝对值不等式![]() 的解集为:
的解集为:![]() 或
或![]() .
.
参照小明的思路,解决下列问题:
(1)请你直接写出下列绝对值不等式的解集.
①![]() 的解集是 ;
的解集是 ;
②![]() 的解集是 .
的解集是 .
(2)求绝对值不等式![]() 的解集.
的解集.
(3)直接写出不等式![]() 的解集是 .
的解集是 .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(2,3),双曲线y=![]() (x>0)的图象经过BC上的点D与AB交于点E,连接DE,若E是AB的中点.
(x>0)的图象经过BC上的点D与AB交于点E,连接DE,若E是AB的中点.
(1)求点D的坐标;
(2)点F是OC边上一点,若△FBC和△DEB相似,求点F的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】把顺序连结四边形各边中点所得的四边形叫中点四边形。
(1)任意四边形的中点四边形是什么形状?为什么?
(2)符合什么条件的四边形,它的中点四边形是菱形?
(3)符合什么条件的四边形,它的中点四边形是矩形?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点C是AB的中点,点D是BC的中点,现给出下列等式:①CD=AC-DB,②CD=![]() AB,③CD=AD-BC,④BD=2AD-AB.其中正确的等式编号是( )
AB,③CD=AD-BC,④BD=2AD-AB.其中正确的等式编号是( )
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com