
科目: 来源: 题型:
【题目】在平面直角坐标系中,二次函数y=x2+bx+c(b,c都是常数)的图象经过点(1,0)和(0,2).
(1)当﹣2≤x≤2时,求y的取值范围.
(2)已知点P(m,n)在该函数的图象上,且m+n=1,求点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校实验课程改革,初三年级设罝了A,B,C,D四门不同的拓展性课程(每位学生只选修其中一门,所有学生都有一门选修课程),学校摸底调査了初三学生的选课意向,并将调查结果绘制成两个不完整的统计图,问该校初三年级共有多少学生?其中要选修B、C课程的各有多少学生?

查看答案和解析>>
科目: 来源: 题型:
【题目】以下是两张不同类型火车的车票(“![]() 次”表示动车,“
次”表示动车,“![]() 次”表示高铁):
次”表示高铁):
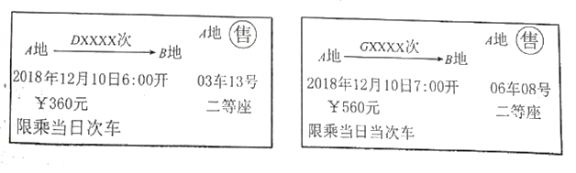
![]() 根据车票中的信息填空:该列动车和高铁是 向而行(填“相”或“同”).
根据车票中的信息填空:该列动车和高铁是 向而行(填“相”或“同”).
![]() 已知该动车和高铁的平均速度分别为
已知该动车和高铁的平均速度分别为![]() ,两列火车的长度不计.经过测算,如果两列火车直达终点(即中途都不停靠任何站点),高铁比动车将早到2
,两列火车的长度不计.经过测算,如果两列火车直达终点(即中途都不停靠任何站点),高铁比动车将早到2![]() .求
.求![]() 两地之间的距离.
两地之间的距离.
查看答案和解析>>
科目: 来源: 题型:
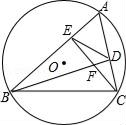
【题目】如图,⊙O的半径为2,弦BC=2![]() ,点A是优弧BC上一动点(不包括端点),△ABC的高BD、CE相交于点F,连结ED.下列四个结论:
,点A是优弧BC上一动点(不包括端点),△ABC的高BD、CE相交于点F,连结ED.下列四个结论:
①∠A始终为60°;
②当∠ABC=45°时,AE=EF;
③当△ABC为锐角三角形时,ED=![]() ;
;
④线段ED的垂直平分线必平分弦BC.
其中正确的结论是_____.(把你认为正确结论的序号都填上)
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年2月,市城区公交车施行全程免费乘坐政策,标志着我市公共交通建设迈进了一个新的时代.下图为某一条东西方向直线上的公交线路,东起职教园区站,西至富士康站,途中共设![]() 个上下车站点,如图所示:
个上下车站点,如图所示:
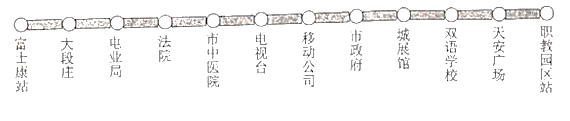
某天,小王从电业局站出发,始终在该线路的公交站点做志愿者服务,到![]() 站下车时,本次志愿者服务活动结束,如果规定向东为正,向西为负,当天的乘车站数按先后顺序依次记录如下(单位:站):
站下车时,本次志愿者服务活动结束,如果规定向东为正,向西为负,当天的乘车站数按先后顺序依次记录如下(单位:站): ![]() ;
;
![]() 请通过计算说明
请通过计算说明![]() 站是哪一站?
站是哪一站?
![]() 若相邻两站之间的平均距离为
若相邻两站之间的平均距离为![]() 千米,求这次小王志愿服务期间乘坐公交车行进的总路程是多少千米?
千米,求这次小王志愿服务期间乘坐公交车行进的总路程是多少千米?
查看答案和解析>>
科目: 来源: 题型:
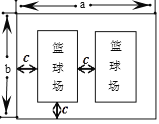
【题目】今年假期某校对操场进行了维修改造,如图是操场的一角.在长为![]() 米,宽为
米,宽为![]() 米的长方形场地中间,并排着两个大小相同的篮球场,这两个篮球场之间以及篮球场与长方形场地边沿的距离都为
米的长方形场地中间,并排着两个大小相同的篮球场,这两个篮球场之间以及篮球场与长方形场地边沿的距离都为![]() 米.
米.
(1)直接写出一个篮球场的长和宽;(用含字母![]() ,
,![]() ,
,![]() 的代数式表示)
的代数式表示)
(2)用含字母![]() ,
,![]() ,
,![]() 的代数式表示这两个篮球场占地面积的和,并求出当
的代数式表示这两个篮球场占地面积的和,并求出当![]() ,
,![]() ,
,![]() 时,这两个篮球场占地面积的和.
时,这两个篮球场占地面积的和.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点A是双曲线y=﹣![]() 在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=
在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=![]() 上运动,则k的值为_____.
上运动,则k的值为_____.

查看答案和解析>>
科目: 来源: 题型:
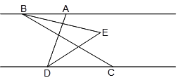
【题目】如图,已知AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E.∠ADC =68°.
(1)求∠EDC的度数;
(2)若∠ABC =n°,求∠BED的度数(用含n的代数式表示);
(3)将线段BC沿DC方向平移, 使得点B在点A的右侧,其他条件不变,画出图形并判断∠BED的度数是否改变,若改变,求出它的度数(用含n的式子表示),不改变,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC与△DCE有公共顶点C,AB=CD,BC=CE,∠ABC=∠DCE=90°.
(1)如图1,当点D在BC延长线上时.
①求证:△ABC≌△DCE.
②判断AC与DE的位置关系,并说明理由.
(2)如图2,△CDE从(1)中位置开始绕点C顺时针旋转,当点D落在BC边上时停止.
①若∠A=60°,记旋转的度数为![]() ,当
,当![]() 为何值时,DE与△ABC一边平行.
为何值时,DE与△ABC一边平行.
②如图3,若AB=c, BC=a, AC=b, a>c,边BC,DE交于点F,求整个运动过程中,F在BC上的运动路程(用含a, b, c的代数式表示)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com