
科目: 来源: 题型:
【题目】已知点A(1,2)为反比例函数![]() 图象上一点,
图象上一点,
(1) 将点A沿x轴正方向平移1个单位,对应点A′的坐标为___________
将比例函数![]() 图象沿x轴正方向平移1个单位,平移后的函数解析式为___________
图象沿x轴正方向平移1个单位,平移后的函数解析式为___________
将比例函数![]() 图象沿x轴正方向平移m个单位,平移后的函数解析式为___________
图象沿x轴正方向平移m个单位,平移后的函数解析式为___________
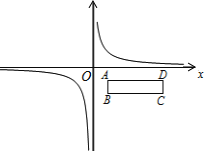
(2) 在平面直角坐标系中,矩形ABCD位置如图,其中A、B、C三点的坐标分别为A(1,-1)、B(1,-2)、C(4,-2).现将反比例函数![]() 图象沿x轴正方向平移,若平移速度为每秒1个单位长度
图象沿x轴正方向平移,若平移速度为每秒1个单位长度
① 设函数图象平移时间为t秒,求函数图象与矩形ABCD有公共点时t的取值范围;
② 在平移过程中,当函数图象与矩形ABCD有公共点时,则函数图象扫过的区域夹在直线AD、BC的图形面积为___________(直接写出答案)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,数轴上![]() ,
,![]() 两点对应的数分别为
两点对应的数分别为![]() 和
和![]() ,点
,点![]() 和点
和点![]() 同时从原点出发,点
同时从原点出发,点![]() 以每秒
以每秒![]() 个单位长度的速度沿数轴正方向运动,点
个单位长度的速度沿数轴正方向运动,点![]() 以每秒
以每秒![]() 个单位长度的速度先沿数轴负方向运动,到达点
个单位长度的速度先沿数轴负方向运动,到达点![]() 后再沿数轴正方向运动,当点
后再沿数轴正方向运动,当点![]() 到达点
到达点![]() 后,两个点同时结束运动.设运动时间为
后,两个点同时结束运动.设运动时间为![]() 秒.
秒.

(1)当![]() 时,求线段
时,求线段![]() 的长度;
的长度;
(2)通过计算说明,当![]() 在不同范围内取值时,线段
在不同范围内取值时,线段![]() 的长度如何用含
的长度如何用含![]() 的式子表示?
的式子表示?
(3)当点![]() 是
是![]() 的中点时直接写出
的中点时直接写出![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
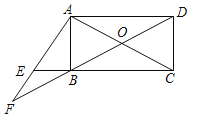
【题目】如图,平行四边形ABCD的对角线AC、BD交于点O,点E在边CB的延长线上,且∠EAC=90°,AE2=EBEC.
(1)求证:四边形ABCD是矩形;
(2)延长DB、AE交于点F,若AF=AC,求证:AE=BF.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下面材料,完成(1)~(2)题:
数学课上,老师出示了一道题:如图1,将一个直角三角板![]() 的直角边
的直角边![]() 摆放在直线
摆放在直线![]() 上,然后以直角顶点
上,然后以直角顶点![]() 为旋转中心顺时针旋转这个三角板.若射线
为旋转中心顺时针旋转这个三角板.若射线![]() 平分
平分![]() 、探究
、探究![]() 和
和![]() 的数量关系,并说明经过一段时间的思考后,同学们开始了交流:
的数量关系,并说明经过一段时间的思考后,同学们开始了交流:
小明:我根据老师的叙述画出图2,并计算出当![]() 时,
时,![]() 的度数是
的度数是![]() ;
;
小红:在小明的图形中,点![]() 、
、![]() 都在
都在![]() 的上方,我发现,在这种情况下,
的上方,我发现,在这种情况下,![]() 始终在
始终在![]() 的内部.若设
的内部.若设![]() 的度数是
的度数是![]() ,通过计算,
,通过计算,![]() 的度数可以用含
的度数可以用含![]() 的式子表示,得到
的式子表示,得到![]() 和
和![]() 的数量关系是
的数量关系是![]() ;
;
小华:我除了画小明的这种图形,还画了其余几种,也分别得出![]() 和
和![]() 的数量关系,从而解决了老师提出的问题.
的数量关系,从而解决了老师提出的问题.
老师:这些同学都先画出图形,再解决问题,这体现了图形的直性,但要注意一点,在初中阶段我们研究的角都是小于![]() 的.随着大家交流的深入,点
的.随着大家交流的深入,点![]() 的位置由
的位置由![]() 上方到直线
上方到直线![]() 外,
外,![]() 的值由数字到字母,这体现了从特殊到一般的思想,同学们再根据小华所说的进行探究,还能归纳出其他的数学思想方法!
的值由数字到字母,这体现了从特殊到一般的思想,同学们再根据小华所说的进行探究,还能归纳出其他的数学思想方法!
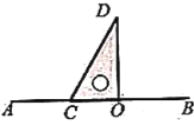
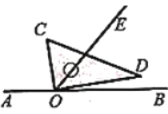
图1 图2
(1)如图2,点![]() 、
、![]() 都在
都在![]() 上方,
上方,![]() .
.
①用含![]() 的代数式表示
的代数式表示![]() 为_____________;
为_____________;
②小红的“![]() 始终在
始终在![]() 的内部”的说法是正确的吗,为什么?
的内部”的说法是正确的吗,为什么?
(2)根据小华的叙述,写出![]() 与
与![]() 的数量关系并说明.
的数量关系并说明.
查看答案和解析>>
科目: 来源: 题型:
【题目】我市晶泰星公司安排![]() 名工人生产甲、乙两种产品,每人每天生产
名工人生产甲、乙两种产品,每人每天生产![]() 件甲产品或
件甲产品或![]() 件乙产品.根据市场行情测得,甲产品每件可获利
件乙产品.根据市场行情测得,甲产品每件可获利![]() 元,乙产品每件可获利
元,乙产品每件可获利![]() 元.而实际生产中,生产乙产品需要数外支出一定的费用,经过核算,每生产
元.而实际生产中,生产乙产品需要数外支出一定的费用,经过核算,每生产![]() 件乙产品,当天每件乙产品平均荻利减少
件乙产品,当天每件乙产品平均荻利减少![]() 元,设每天安排
元,设每天安排![]() 人生产乙产品.
人生产乙产品.
(1)根据信息填表:
产品种类 | 每天工人数(人) | 每天产量(件) | 每件产品可获利润(元) |
甲 |
| ||
乙 |
|
|
(2)若每天生产甲产品可获得的利润比生产乙产品可获得的利润多![]() 元,试问:该企业每天生产甲、乙产品可获得总利润是多少元?
元,试问:该企业每天生产甲、乙产品可获得总利润是多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】一个水果市场某品种苹果的销售方式如下表:
购买苹数量(千克) | 不超过 | 超过 |
每千克的价格(元) |
|
|
(1)如果小明购买![]() 千克的苹果,那么他需要付___________元.
千克的苹果,那么他需要付___________元.
(2)小明分两次共购买![]() 千克的苹果,第二次购买的数量多于第一次购买的数量,若他两次共付
千克的苹果,第二次购买的数量多于第一次购买的数量,若他两次共付![]() 元,求他两次分别购买苹果的数量.
元,求他两次分别购买苹果的数量.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数轴上三点M,O,N对应的数分别为-1,0,3,点P为数轴上任意一点,其对应的数为x.
![]()
(1)MN的长为 ;
(2)如果点P到点M、点N的距离相等,那么x的值是 ;
(3)数轴上是否存在点P,使点P到点M、点N的距离之和是8?若存在,直接写出x的值;若不存在,请说明理由.
(4)如果点P以每分钟1个单位长度的速度从点O向左运动,同时点M和点N分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动.设t分钟时点P到点M、点N的距离相等,求t的值.
查看答案和解析>>
科目: 来源: 题型:
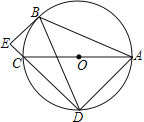
【题目】如图,⊙O是△ABC的外接圆,AC为直径,BD=BA,BE⊥DC交DC的延长线于点E
(1) 求证:BE是⊙O的切线
(2) 若EC=1,CD=3,求cos∠DBA
查看答案和解析>>
科目: 来源: 题型:
【题目】学生对待学习的态度一直是教育工作者关注的问题之一.为此,某区教委对该区部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:

(1)此次抽样调查中,共调查了 名学生;
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】某市水果批发部门欲将A市的一批水果运往本市销售,有火车和汽车两种运输方式,运输过程中的损耗均为200元/时。其它主要参考数据如下:
运输工具 | 途中平均速度(千米/时) | 运费(元/千米) | 装卸费用(元) |
火车 | 100 | 15 | 2000 |
汽车 | 80 | 20 | 900 |
(1)如果汽车的总支出费用比火车费用多1100元,你知道本市与A市之间的路程是多少千米吗?请你列方程解答.
(2)如果A市与某市之间的距离为S千米,且知道火车与汽车在路上耽误的时间分别为2小时和3.1小时,你若是某市水果批发部门的经理,要将这种水果从A市运往本市销售。你将选择哪种运输方式比较合算呢?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com