
科目: 来源: 题型:
【题目】2019年11月铜陵举办了国际半程马拉松比赛,吸引了大批运动爱好者.某商场看准时机,想订购一批![]() 款运动鞋,现有甲,乙两家供应商,它们均以每双
款运动鞋,现有甲,乙两家供应商,它们均以每双![]() 元的价格出售
元的价格出售![]() 款运动鞋,其中供应商甲一律九折销售, 与购买数量无关;而供应商乙规定:购买数量在
款运动鞋,其中供应商甲一律九折销售, 与购买数量无关;而供应商乙规定:购买数量在![]() 双以内(包含
双以内(包含![]() 双),以每双200元的原价出售,当购买数量超出
双),以每双200元的原价出售,当购买数量超出![]() 双时,其超出部分按原价的八折出售.问:
双时,其超出部分按原价的八折出售.问:
![]() 某商场购买多少双时,去两个供应商处的进货价钱一样多?
某商场购买多少双时,去两个供应商处的进货价钱一样多?
![]() 若该商场分两次购买运动鞋,第一次购进
若该商场分两次购买运动鞋,第一次购进![]() 双,第二次购进的数量是第次的
双,第二次购进的数量是第次的![]() 倍多
倍多![]() 双,如果你是商场经理,在两次分开购买的情况下,你预计花多少元采购运动鞋,才能使得商场花销最少?
双,如果你是商场经理,在两次分开购买的情况下,你预计花多少元采购运动鞋,才能使得商场花销最少?
查看答案和解析>>
科目: 来源: 题型:
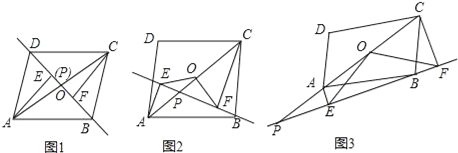
【题目】已知:点P是平行四边形ABCD对角线AC所在直线上的一个动点(点P不与点A、C重合),分别过点A、C向直线BP作垂线,垂足分别为点E、F,点O为AC的中点.(1)当点P与点O重合时如图1,易证OE=OF(不需证明)
(2)直线BP绕点B逆时针方向旋转,当∠OFE=30°时,如图2、图3的位置,猜想线段CF、AE、OE之间有怎样的数量关系?请写出你对图2、图3的猜想,并选择一种情况给予证明.
查看答案和解析>>
科目: 来源: 题型:
【题目】一组连续奇数按如图方式排列,请你解决下列问题:

![]() 第
第![]() 行最后一个数字是___________,在第
行最后一个数字是___________,在第![]() 行第
行第![]() 列的数字是_______________
列的数字是_______________
![]() 请用含
请用含![]() 的代数式表示第
的代数式表示第![]() 行的第
行的第![]() 个数字和最后一个数字;
个数字和最后一个数字;
![]() 现用一个正方形框去围出相邻两行中的
现用一个正方形框去围出相邻两行中的![]() 个数字(例如:第
个数字(例如:第![]() 行和第
行和第![]() 行的
行的![]() ),请问能否在第
),请问能否在第![]() 行和第
行和第![]() 行中求出
行中求出![]() 个数字的和是
个数字的和是![]() ?若能,请求出这
?若能,请求出这![]() 个数字;若不能,请说明理由.
个数字;若不能,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是∠BAC的平分线.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是( )

A. ![]() B. 4 C.
B. 4 C. ![]() D. 5
D. 5
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABE、△ADC和△ABC分别是关于AB,AC边所在直线的轴对称图形,若∠1:∠2:∠3=7:2:1,则∠α的度数为( ).

A.126°B.110°C.108°D.90°
查看答案和解析>>
科目: 来源: 题型:
【题目】某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示:
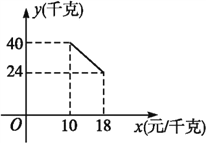
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)求每天的销售利润W(元)与销售价x(元/千克)之间的函数关系式.当销售价为多少时,每天的销售利润最大?最大利润是多少?
(3)该经销商想要每天获得168元的销售利润,销售价应定为多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,点D、E分别在AC、BC上,且CD·BC=AC·CE,以E为圆心,DE长为半径作圆,⊙E经过点B,与AB、BC分别交于点F、G.
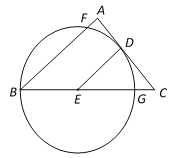
(1)求证:AC是⊙E的切线;
(2)若AF=4,CG=5,求⊙E的半径;
(3)若Rt△ABC的内切圆圆心为I,求⊙I的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】随着近几年我市私家车日越增多,超速行驶成为引发交通事故的主要原因之一.某中学数学活动小组为开展“文明驾驶、关爱家人、关爱他人”的活动,设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点P,在笔直的车道m上确定点O,使PO和m垂直,测得PO的长等于21米,在m上的同侧取点A、B,使∠PAO=30°,∠PBO=60°.
(1)求A、B之间的路程(保留根号);
(2)已知本路段对校车限速为12米/秒若测得某校车从A到B用了2秒,这辆校车是否超速?请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】小美周末来到公园,发现在公园一角有一种“守株待兔”游戏.游戏设计者提供了一只兔子和一个有A、B、C、D、E五个出入口的兔笼,而且笼内的兔子从每个出入口走出兔笼的机会是均等的.规定:
①玩家只能将小兔从A、B两个出入口放入;
②如果小兔进入笼子后选择从开始进入的出入口离开,则可获得一只价值5元小兔玩具,否则应付费3元.
(1)问小美得到小兔玩具的机会有多大?
(2)假设有100人次玩此游戏,估计游戏设计者可赚多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com