
科目: 来源: 题型:
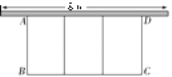
【题目】如图,在一面靠墙的空地上用长为24 m的篱笆围成中间隔有二道篱笆的长方形花圃.设花圃的宽AB为x m,面积为S m2.
(1)求S与x的函数关系式及自变量的取值范围;
(2)已知墙的最大可用长度为8 m,
①求所围成花圃的最大面积;
②若所围花圃的面积不小于20 m2,请直接写出x的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点O在直线MN上,过点O作射线OP,使∠MOP=130°,将一块直角三角板的直角顶点始终放在点O处.
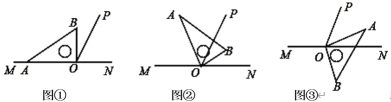
(1)如图①,当三角板的一边OA在射线OM上,另一边OB在直线MN的上方时,求∠POB的度数;
(2)若将三角板绕点O旋转至图②所示的位置,此时OB恰好平分∠PON,求∠BOP和∠AOM 的度数;
(3)若将三角板绕点O旋转至图③所示位置,此时OA在∠PON 的内部,若OP所在的直线平分∠MOB,求∠POA 的度数;
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点P从(0,3)出发,沿所示的方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点p第2019次碰到矩形的边时点P的坐标为( )

A. ( 1,4 )B. ( 5,0 )C. ( 8,3 )D. ( 6,4 )
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,△ABC的边BC在x轴上,A,C两点的坐标分别为A(0,m),C(n,0),B(﹣5,0),且(n﹣3)2+![]() =0.一动点P从点B出发,以每秒2单位长度的速度沿射线BO匀速运动,设点P运动的时间为ts.
=0.一动点P从点B出发,以每秒2单位长度的速度沿射线BO匀速运动,设点P运动的时间为ts.
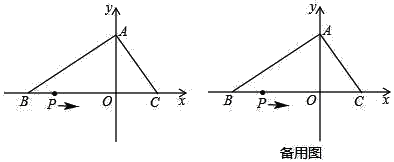
(1)求A,C两点的坐标;
(2)连接PA,若△PAB为等腰三角形,求点P的坐标;
(3)当点P在线段BO上运动时,在y轴上是否存在点Q,使△POQ与△AOC全等?若存在,请求出t的值并直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】(7分)如图,已知抛物线y=x2+bx+c经过A(-1,0),B(3,0)两点.
(1)求抛物线的解析式和顶点坐标;
(2)当0<x<3时,求y的取值范围;
(3)点P为抛物线上一点,若S△PAB=10,求出此时点P的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知点C是线段AB的中点
(1)如图,若点D在线段CB上,且BD=1.5厘米,AD=6.5厘米,求线段CD的长度;
![]()
(2)若将(1)中的“点D在线段CB上”改为“点D在线段CB的延长线上”,其他条件不变,请画出相应的示意图,并求出此时线段CD的长度.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数y=3x2+36x+81.
(1)写出它的顶点坐标;
(2)当x取何值时,y随x的增大而增大;
(3)求出图象与x轴的交点坐标;
(4)当x取何值时,y有最小值,并求出最小值;
(5)当x取何值时,y<0.
查看答案和解析>>
科目: 来源: 题型:
【题目】新定义:我们把两个面积相等但不全等的三角形叫做偏等积三角形.
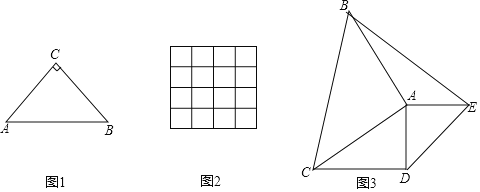
(1)初步尝试:如图1,已知等腰直角△ABC,∠ACB=90°,请用直尺和圆规将它分成两个三角形,使它们成为偏等积三角形,请保留作图痕迹.
(2)理解运用:请在图2的方格纸中,画两个面积为2的三角形,使这两个三角形是偏等积三角形.
(3)综合应用:如图3,已知△ACD为直角三角形,∠ADC=90°,以AC,AD为腰向外作等腰直角三角形ABC和等腰直角三角形ADE,∠CAB=∠DAE=90°,连结BE,求证:△ACD与△ABE为偏等积三角形.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在矩形OABC 中,OA=5,AB=4,点D 为边AB 上一点,将△BCD 沿直线CD 折叠,使点B 恰好落在OA边上的点E 处,分别以OC,OA 所在的直线为x 轴,y 轴建立平面直角坐标系.
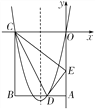
(1)求OE 的长;
(2)求经过O,D,C 三点的抛物线的表达式;
(3)一动点P从点C 出发,沿CB以每秒2 个单位长的速度向点B运动,同时动点Q从E 点出发,沿EC以每秒1个单位长的速度向点C运动,当点P到达点B时,两点同时停止运动.设运动时间为t s,当t为何值时,DP=DQ.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com