
科目: 来源: 题型:
【题目】如图,在ABCD中,AE,CF分别是∠BAD和∠BCD的平分线,添加一个条件,仍无法判断四边形AECF为菱形的是( )

A. AE=AFB. EF⊥ACC. ∠B=60°D. AC是∠EAF的平分线
查看答案和解析>>
科目: 来源: 题型:
【题目】某巡逻车在一条南北大道上巡逻,某天巡逻车从岗亭A处出发,规定向北方向为正,向南方向为负,当天行驶记录如下(单位:千米) ![]() .
.
(1)最终巡逻车是否回到岗亭![]() 处?若没有,请描述巡逻车的位置:
处?若没有,请描述巡逻车的位置:
(2)若巡逻车行驶1千米耗油0.1升,出发时油箱有油5升,请问途中需要加油吗?若需要,途中至少还需补充多少升油?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知四边形ABCD的对角线AC,BD互相垂直,则下列条件能判定四边形ABCD为菱形的是( )
A. AC,BD互相平分
B. BA=BC
C. AC=BD
D. AB∥CD
查看答案和解析>>
科目: 来源: 题型:
【题目】若一个三位数百位上数字是![]() ,十位上数字是
,十位上数字是![]() .个位上数字是
.个位上数字是![]() ,则这个三位数可记作
,则这个三位数可记作![]()
(1)若一个两位数![]() .满足关系式
.满足关系式![]() .
.
①试求出![]() 的数量关系:
的数量关系:
②请直接写出满足关系式![]() 的所有两位数.
的所有两位数.
(2)将一个三位数![]() ,其中
,其中![]() .现将三位数
.现将三位数![]() 中间数字
中间数字![]() 去掉,成为一个两位数
去掉,成为一个两位数![]() 且满足
且满足![]() .请直接写出所有符合条件的三位数.
.请直接写出所有符合条件的三位数.
查看答案和解析>>
科目: 来源: 题型:
【题目】依次剪6张正方形纸片拼成如图示意的图形,图形中正方形①的面积为1,正方形②的面积为![]() .
.
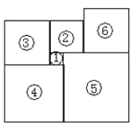
(1)请用含![]() 的式子直接写出正方形⑤的面积;
的式子直接写出正方形⑤的面积;
(2)若正方形⑥与正方形③的面积相等,求正方形④和正方形⑤的面积比.
查看答案和解析>>
科目: 来源: 题型:
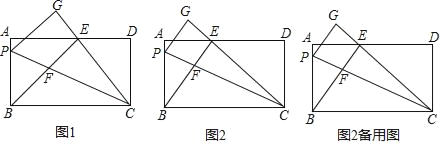
【题目】在矩形ABCD中,AB=12,P是边AB上一点,把△PBC沿直线PC折叠,顶点B的对应点是点G,过点B作BE⊥CG,垂足为E且在AD上,BE交PC于点F.
(1)如图1,若点E是AD的中点,求证:△AEB≌△DEC;
(2)如图2,①求证:BP=BF;
②当AD=25,且AE<DE时,求cos∠PCB的值;
③当BP=9时,求BEEF的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,等边△ABC沿射线BC向右平移到△DCE的位置,连结AD,BD,则下列结论:①AD=BC;②BD,AC互相平分;③四边形ACED是菱形;④BD=BE;其中正确的个数是( )

A.0个B.1个C.2个D.3个
查看答案和解析>>
科目: 来源: 题型:
【题目】某市创建“绿色发展模范城市”,针对境内长江段两种主要污染源:生活污水和沿江工厂污染物排放,分别用“生活污水集中处理”(下称甲方案)和“沿江工厂转型升级”(下称乙方案)进行治理,若江水污染指数记为Q,沿江工厂用乙方案进行一次性治理(当年完工),从当年开始,所治理的每家工厂一年降低的Q值都以平均值n计算.第一年有40家工厂用乙方案治理,共使Q值降低了12.经过三年治理,境内长江水质明显改善.
(1)求n的值;
(2)从第二年起,每年用乙方案新治理的工厂数量比上一年都增加相同的百分数m,三年来用乙方案治理的工厂数量共190家,求m的值,并计算第二年用乙方案新治理的工厂数量;
(3)该市生活污水用甲方案治理,从第二年起,每年因此降低的Q值比上一年都增加个相同的数值a.在(2)的情况下,第二年,用乙方案所治理的工厂合计降低的Q值与当年因甲方案治理降低的Q值相等,第三年,用甲方案使Q值降低了39.5.求第一年用甲方案治理降低的Q值及a的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】点![]() 为数轴上的两点,点
为数轴上的两点,点![]() 对应的数为
对应的数为![]() ,点
,点![]() 对应的数为3,
对应的数为3,![]() .
.
(1)求![]() 两点之间的距离;
两点之间的距离;
(2)若点![]() 为数轴上的一个动点,其对应的数记为
为数轴上的一个动点,其对应的数记为![]() ,试猜想当
,试猜想当![]() 满足什么条件时,点
满足什么条件时,点![]() 到
到![]() 点的距离与点
点的距离与点![]() 到
到![]() 点的距离之和最小.请写出你的猜想,并说明理由:
点的距离之和最小.请写出你的猜想,并说明理由:
(3)若![]() 为数轴上的两个动点(
为数轴上的两个动点(![]() 点在
点在![]() 点右侧),
点右侧), ![]() 两点之间的距离为
两点之间的距离为![]() ,当点
,当点![]() 到A点的距离与点
到A点的距离与点![]() 到
到![]() 点的距离之和有最小值4时,
点的距离之和有最小值4时,![]() 的值为_________.
的值为_________.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读思考,完成下列填空.
问题提出:
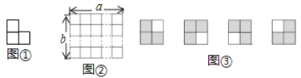
如图,图①是一张由三个边长为1的小正方形组成的![]() 形纸片.图②是张
形纸片.图②是张![]() 的方格纸(
的方格纸(![]() 的方格纸指边长分别为
的方格纸指边长分别为![]() 的长方形,被分成
的长方形,被分成![]() 个边长为1的小正方形,其中
个边长为1的小正方形,其中![]() ,且
,且![]() 为正整数).把图①放置在图②中.使它恰好盖住图②中的三个小正方形,共有多少种不同的放置方法?
为正整数).把图①放置在图②中.使它恰好盖住图②中的三个小正方形,共有多少种不同的放置方法?
问题探究;
探究一:把图①放置在![]() 的方格纸中,使它恰好盖住其中的三个小正方形,如图③,显然有4种不同的放置方法.
的方格纸中,使它恰好盖住其中的三个小正方形,如图③,显然有4种不同的放置方法.
探究二:把图①放置在![]() 的方格纸中,使它恰好盖住其中的三个小正方形.如图④,在
的方格纸中,使它恰好盖住其中的三个小正方形.如图④,在![]() 的方格纸中,共可以找到2个位置不同的
的方格纸中,共可以找到2个位置不同的![]() 方格,依据探究一的结论可知,把图①放置在
方格,依据探究一的结论可知,把图①放置在![]() 的方格纸中.使它恰好盖住其中的三个小正方形,共有_____种不同的放置方法.
的方格纸中.使它恰好盖住其中的三个小正方形,共有_____种不同的放置方法.
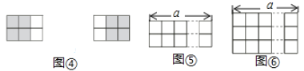
探究三:把图①放置在![]() 的方格纸中,使它恰好盖住其中的三个小正方形,如图⑤,在
的方格纸中,使它恰好盖住其中的三个小正方形,如图⑤,在![]() 的方格纸中,共可以找到_______个位置不同的
的方格纸中,共可以找到_______个位置不同的![]() 方格,依据探究一的结论可知,把图①放置在
方格,依据探究一的结论可知,把图①放置在![]() 的方格纸中,使它恰好盖住其中的三个小正方形,共有________种不同的放置方法.
的方格纸中,使它恰好盖住其中的三个小正方形,共有________种不同的放置方法.
探究四:把图①放置在![]() 的方格纸中,使它恰好盖住其中的三个小正方形,如图⑥,在
的方格纸中,使它恰好盖住其中的三个小正方形,如图⑥,在![]() 的方格纸中,共可以找到_______个位置不同的
的方格纸中,共可以找到_______个位置不同的![]() 方格,依据探究一的结论可知,把图①放置在
方格,依据探究一的结论可知,把图①放置在![]() 的方格纸中,使它恰好盖住其中的三个小正方形共有________种不同的放置方法.
的方格纸中,使它恰好盖住其中的三个小正方形共有________种不同的放置方法.
……
问题解决:
把图①放置在![]() 的方格纸中,使它恰好盖住其中的三个小正方形,共有_________种不同的放置方法.
的方格纸中,使它恰好盖住其中的三个小正方形,共有_________种不同的放置方法.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com