
科目: 来源: 题型:
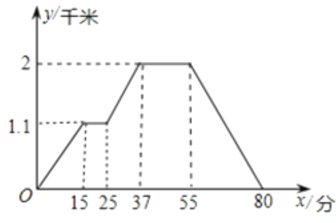
【题目】如图,反映的过程是小涛从家出发,去菜地浇水,又去玉米地锄草,然后回家.其中x表示时间,y表示小涛离家的距离.
(1)菜地离小涛家的距离是________km,小涛走到菜地用了_______min,小涛给菜地浇水用了_______min;
(2)小涛从菜地到玉米地用了____min,小涛给玉米地锄草用了________ min;
(3)玉米地离小涛家的距离是________km,小涛从玉米地走回家的平均速度是_____________.
查看答案和解析>>
科目: 来源: 题型:
【题目】高速公路养护小组乘车沿东西向公路巡视维护,如果约定向东为正,向西为负,当天的行驶记录如下(单位:千米):+10,-9,+8,-12,-3,7,-6,-7,6,+4.
(1)养护小组最后到达的地方在出发点的哪个方向?距出发点多远?
(2)若汽车行驶每千米耗油量为0.4升,求这一天养护小组的汽车共耗油多少升?
查看答案和解析>>
科目: 来源: 题型:
【题目】永祚寺双塔,又名凌霄双塔,是山西省会太原现存古建筑中最高的建筑,位于太原市城区东南向山脚畔.数学活动小组的同学对其中一个塔进行了测量.测量方法如下:如图所示,间接测得该塔底部点B到地面上一点E的距离为48 m,塔的顶端为点A,且AB⊥CB,在点E处竖直放一根标杆,其顶端为D,在BE的延长线上找一点C,使C,D,A三点在同一直线上,测得CE=2 m.
(1)方法1,已知标杆DE=2.2 m,求该塔的高度;
(2)方法2,测量得∠ACB=47.5°,已知tan47.5°≈1.09,求该塔的高度;
(3)假如该塔的高度在方法1和方法2测得的结果之间,你认为该塔的高度大约是多少米?


查看答案和解析>>
科目: 来源: 题型:
【题目】(1)探索材料1(填空):
数轴上表示数![]() 和数
和数![]() 的两点之间的距离等于
的两点之间的距离等于![]() .例如数轴上表示数2和5的两点距离为
.例如数轴上表示数2和5的两点距离为![]() ;数轴上表示数3和-1的两点距离为
;数轴上表示数3和-1的两点距离为![]() ;则
;则![]() 的意义可理解为数轴上表示数 和 这两点的距离;
的意义可理解为数轴上表示数 和 这两点的距离;![]() 的意义可理解为数轴上表示数 和 这两点的距离;
的意义可理解为数轴上表示数 和 这两点的距离;
(2)探索材料2(填空):
①如图1,在工厂的一条流水线上有两个加工点![]() 和
和![]() ,要在流水线上设一个材料供应点
,要在流水线上设一个材料供应点![]() 往两个加工点输送材料,材料供应点
往两个加工点输送材料,材料供应点![]() 应设在 才能使
应设在 才能使![]() 到
到![]() 的距离与
的距离与![]() 到
到![]() 的距离之和最小?
的距离之和最小?

②如图2,在工厂的一条流水线上有三个加工点![]() 要在流水线上设一个材料供应点
要在流水线上设一个材料供应点![]() 往三个加工点输送材料,材料供应点
往三个加工点输送材料,材料供应点![]() 应设在 才能使
应设在 才能使![]() 到
到![]() 三点的距离之和最小?
三点的距离之和最小?

③如图3,在工厂的一条流水线上有四个加工点![]() ,要在流水线上设一个材料供应点
,要在流水线上设一个材料供应点![]() 往四个加工点输送材料,材料供应点
往四个加工点输送材料,材料供应点![]() 应设在 才能使
应设在 才能使![]() 到
到![]() 四点的距离之和最小?
四点的距离之和最小?

(3)结论应用(填空):
①代数式![]() 的最小值是 ,此时
的最小值是 ,此时![]() 的范围是 ;
的范围是 ;
②代数式![]() 的最小值是 ,此时
的最小值是 ,此时![]() 的值为 .
的值为 .
③代数式![]() 的最小值是 ,此时
的最小值是 ,此时![]() 的范围是 .
的范围是 .
查看答案和解析>>
科目: 来源: 题型:
【题目】图1所示是一枚质地均匀的骰子.骰子有六个面并分别代表数字1,2,3,4,5,6.如图2,正六边形ABCDEF的顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子向上的一面上的点数是几,就沿正六边形的边顺时针方向连续跳几个边长.如:若从圈A起跳,第一次掷得3,就顺时针连续跳3个边长,落到圈D;若第二次掷得2,就从圈D开始顺时针连续跳2个边长,落到圈F……
设游戏者从圈A起跳.
(1)小明随机掷一次骰子,求落回到圈A的概率P1;
(2)小亮随机掷两次骰子,用列表法或画树状图法求最后落回到圈A的概率P2,并指出他与小明落回到圈A的可能性一样吗?
 图1
图1 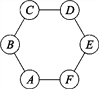 图2
图2
查看答案和解析>>
科目: 来源: 题型:
【题目】△ABC底边BC上的高为16 cm,当BC的长x(cm)从小到大变化时,△ABC的面积y(cm2)也随之发生变化.
(1)在这个变化过程中,常量是________,自变量是________,因变量是_________;
(2)写出y与x之间的关系式为_______________;
(3)当x=5 cm时,y=________cm2;当x=15 cm时,y=________cm2;y随x的增大而__________.
查看答案和解析>>
科目: 来源: 题型:
【题目】在等边△ABC的顶点A、C处各有一只蜗牛,它们同时出发,分别以每分钟1米的速度由A向B和由C向A爬行,其中一只蜗牛爬到终点时,另一只也停止运动,经过t分钟后,它们分别爬行到D、E处,请问:
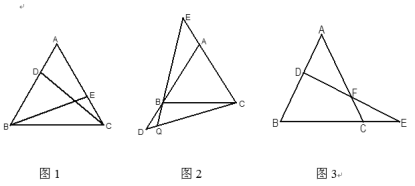
(1)如图1,在爬行过程中,CD和BE始终相等吗?
(2)如果将原题中的“由A向B和由C向A爬行”,改为“沿着AB和CA的延长线爬行”,EB与CD交于点Q,其他条件不变,蜗牛爬行过程中∠CQE的大小保持不变,请利用图2说明:∠CQE=60°;
(3)如果将原题中“由C向A爬行”改为“沿着BC的延长线爬行,连接DE交AC于F”,其他条件不变,如图3,则爬行过程中,DF始终等于EF是否正确?
查看答案和解析>>
科目: 来源: 题型:
【题目】甲,乙两家服装商店销售同一品牌的西装和领带,西装定价都是每套200元,领带定价都是每条40元.现两家商店都在促销:甲店:买一套西装送一条领带;乙店:西装和领带都按定价的90%付款.
学校合唱团要购买西装20套,领带![]() 条(
条(![]() ),由后勤谢老师负责购买,请为谢老师出谋划策:
),由后勤谢老师负责购买,请为谢老师出谋划策:
(1)若只在一家商店购买,当![]() 时,谢老师选择哪家商店购买西装和领带更划算?
时,谢老师选择哪家商店购买西装和领带更划算?
(2)若只在一家商店购买,请用含![]() 的代数式分别表示在两家商店的花费;
的代数式分别表示在两家商店的花费;
(3)当![]() 时,请设计最省钱的购买方案并求出最少的花费是多少.
时,请设计最省钱的购买方案并求出最少的花费是多少.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,且交OE于点F.
(1)求证:OE是CD的垂直平分线.
(2)若∠AOB=60,请你探究OE,EF之间有什么数量关系?并证明你的结论。

查看答案和解析>>
科目: 来源: 题型:
【题目】自我国实施“限塑令”起,开始有偿使用环保购物袋,为了满足市场需求,某厂家生产A、B两种款式的布质环保购物袋,每天生产4500个,两种购物袋的成本和售价如下表,若设每天生产A种购物袋 x个.
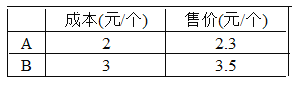
(1)用含x的整式表示每天的生产成本,并进行化简;
(2)用含x的整式表示每天获得的利润,并进行化简(利润=售价-成本);
(3)当x=1500时,求每天的生产成本与每天获得的利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com