
科目: 来源: 题型:
【题目】阅读下面材料
在数学课上,老师提出如下问题:
己知:已知:Rt△ABC,∠ABC=90°.
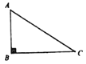
求作:矩形ABCD.
小敏的作法如下:
①以A为圆心,BC长为半径作弧,以C为圆心,AB长为半径作弧,两弧相交于点D;
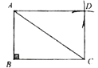
②连接DA、DC;所以四边形ABCD为所求矩形.
老师说:“小敏的作法正确.”
请回答:小敏的作法正确的理由是____________________.
查看答案和解析>>
科目: 来源: 题型:
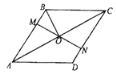
【题目】如图,在菱形ABCD中,点M、 N分别在AB、CD上,AM=CN, MN与AC交于点O,连接BO,若∠BAC=29°,则∠OBC为________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AD为△ABC的中线,BE为△ABD的中线.
(1)若∠ABE=15°,∠BAD=40°,则∠BED=________°;
(2)请在图中作出△BED中BD边上的高EF;
(3)若△ABC的面积为40,BD=5,则点E到BC边的距离为多少?

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD=5,BC=CD且BC>AB,BD=8.给出以下判断:
①AC垂直平分BD;
②四边形ABCD的面积S=ACBD;
③顺次连接四边形ABCD的四边中点得到的四边形可能是正方形;
④当A,B,C,D四点在同一个圆上时,该圆的半径为![]() ;
;
⑤将△ABD沿直线BD对折,点A落在点E处,连接BE并延长交CD于点F,当BF⊥CD时,点F到直线AB的距离为![]() .
.
其中正确的是_____.(写出所有正确判断的序号)

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,分别用火柴棍连续搭建正三角形和正六边形,公共边只用一根火柴棍.如果搭建正三角形和正六边形共用了2018根火柴棍,并且正三角形的个数比正六边形的个数多7个,那么能连续搭建正三角形的个数是_____.

查看答案和解析>>
科目: 来源: 题型:
【题目】数学课上,陈老师对我们说,如果1条线段将一个三角形分成2个等腰三角形,那么这1条线段就称为这个三角形的“好线”,如果2条线段将一个三角形分成3个等腰三角形,那么这2条线段就称为这个三角形的“好好线”.
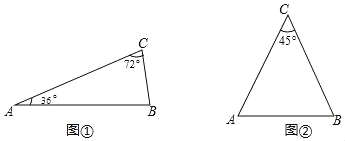
(1)如图①,在△ABC中,∠A=36°,∠C=72°,请你在这个三角形中画出它的“好线”,并标出等腰三角形顶角的度数.
(2)如图②,已知△ABC是一个顶角为45°的等腰三角形,请你在这个三角形中画出它的“好好线”,并标出所分得的等腰三角形底角的度数.
(应用)
(3)在△ABC中,已知一个内角为42°,若它只有“好线”,请你写出这个三角形最大内角的度数:___ ___ (写出其中两种情形即可)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=50°时,求∠DEF的度数.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=20°,∠ACP=50°,则∠A+∠P=( )

A.70°B.80°C.90°D.100°
查看答案和解析>>
科目: 来源: 题型:
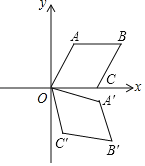
【题目】如图,在平面直角坐标系xOy中,菱形OABC的边长为2,点A在第一象限,点C在x轴正半轴上,∠AOC=60°,若将菱形OABC绕点O顺时针旋转75°,得到四边形OA′B′C′,则点B的对应点B′的坐标为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com