
科目: 来源: 题型:
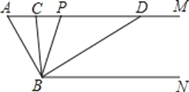
【题目】如图,已知AM∥BN,∠A=60°.点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)求∠CBD的度数;
(2)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,直接写出∠ABC的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】在前面的学习中,我们通过对同一面积的不同表达和比较,根据图①和图②发现并验证了平方差公式和完全平方公式.这种利用面积关系解决问题的方法,使抽象的数量关系因几何直观而形象化.
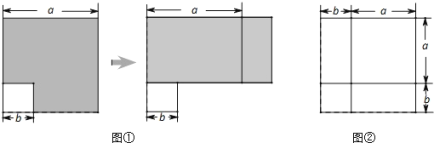
请你利用上述方法解决下列问题:
(1)请写出图1和图2所表示的代数恒等式
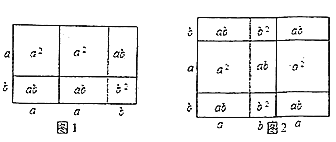
_______ _______
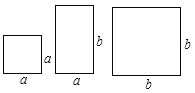
(2)现有a×a,b×b的正方形纸片和a×b的矩形纸片各若干块,试选用这些纸片(每种纸片至少用一次,每两个纸片之间既不重叠,也无空隙,拼出的图形中必须保留拼图的痕迹),使拼出的矩形面积为为2a2+5ab+2b2,并标出此矩形的长和宽.
(拓展应用)
提出问题:47×43,56×54,79×71,…是一些十位数字相同,且个位数字之和是10的两个两位数相乘的算式,是否可以找到一种速算方法?
几何建模:用矩形的面积表示两个正数的乘积,以47×43为例:
(1)画长为47,宽为43的矩形,如图③,将这个47×43的矩形从右边切下长40,宽3的一条,拼接到原矩形上面.
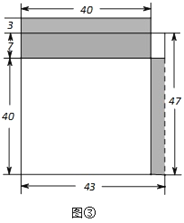
(2)原矩形面积可以有两种不同的表达方式:47×43的矩形面积或(40+7+3)×40的矩形与右上角3×7的矩形面积之和,47×43=(40+10)×40+3×7=5×4×100+3×7=2021,
用文字表述47×43的速算方法是:十位数字4加1的和与4相乘,再乘以100,加上个位数字3与7的积,构成运算结果.
归纳提炼:
两个十位数字相同,并且个位数字之和是10的两位数相乘的速算方法是(用文字表述)_________.
证明上述速算方法的正确性;
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在正方形ABCD中,对角线AC,BD交于点0,过点0的直线分别交边AD,BC于点E,F,EF=6.则AE2+BF2的值为( )
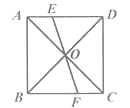
A. 9 B. 16 C. 18 D. 36
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,半径为1的![]() 的圆心A在抛物线y=(x-3)2-1上,AB//x轴交
的圆心A在抛物线y=(x-3)2-1上,AB//x轴交 ![]() 于点B(点B在点A的右侧),当点A在抛物线上运动时,点B随之运动得到的图象的函数表达式为( )
于点B(点B在点A的右侧),当点A在抛物线上运动时,点B随之运动得到的图象的函数表达式为( )

A. y=(x-4)2-1 B. y=(x-3)2 C. y=(x-2)2-1 D. y=(x-3)2-2
查看答案和解析>>
科目: 来源: 题型:
【题目】已知 ![]() ABC(如图1),按图2所示的尺规作图痕迹不需借助三角形全等就能推出四边形ABCD是平行四边形的依据是( )
ABC(如图1),按图2所示的尺规作图痕迹不需借助三角形全等就能推出四边形ABCD是平行四边形的依据是( )
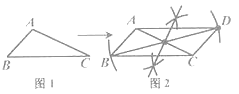
A. 两组对边分别平行的四边形是平行四边形 B. 两组对边分别相等的四边形是平行四边形
C. 一组对边平行且相等的四边形是平行四边形 D. 对角线互相平分的四边形是平行四边形
查看答案和解析>>
科目: 来源: 题型:
【题目】周末,小明坐公交车到滨海公园游玩,他从家出发0.8小时候达到中心书城,逗留一段时间后继续坐公交车到滨海公园,小明离家一段时间后,爸爸驾车沿相同的路线前往海滨公园,并比小明早到达,已知爸爸的平均速度是小明从家到中心书城平均速度的两倍.如图是他们离家路程s(km)与小明离家时间t(h)的关系图,请根据图回答下列问题:
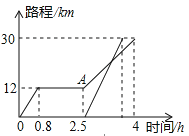
(1)小明家到滨海公园的路程为 km,小明在中心书城逗留的时间为 h;
(2)小明从中心书城到滨海公园的平均速度是 km/h,
(3)小明爸爸比小明早到达多长时间?
(4)爸爸驾车经过多长时间追上小明?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,∠l=∠2,DE⊥BC,AB⊥BC,那么∠A=∠3吗?说明理由.

解:∠A=∠3,理由如下:
∵DE⊥BC,AB⊥BC(已知)
∴∠DEB=∠ABC=90° ( )
∴∠DEB+( )=180°
∴DE∥AB ( )
∴∠1=∠A( )
∠2=∠3( )
∵∠l=∠2(已知)
∴∠A=∠3( )
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,将二次函数y=x2+2x+1的图象沿x轴翻折,然后向右平移1个单位,再向上平移4个单位,得到二次函数y=ax2+bx+c的图象.函数y=x2+2x+1的图象的顶点为点A.函数y=ax2+bx+c的图象的顶点为点B,和x轴的交点为点C,D(点D位于点C的左侧).
(1)求函数y=ax2+bx+c的解析式;
(2)从点A,C,D三个点中任取两个点和点B构造三角形,求构造的三角形是等腰三角形的概率;
(3)若点M是线段BC上的动点,点N是△ABC三边上的动点,是否存在以AM为斜边的Rt△AMN,使△AMN的面积为△ABC面积的![]() ?若存在,求tan∠MAN的值;若不存在,请说明理由.
?若存在,求tan∠MAN的值;若不存在,请说明理由.
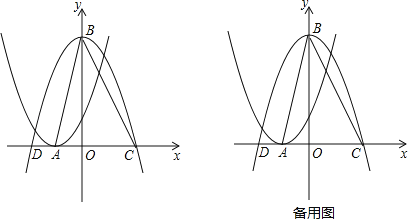
查看答案和解析>>
科目: 来源: 题型:
【题目】已知△ABC中,∠BAC=100°.
(1)若∠ABC和∠ACB的角平分线交于点O,如图1所示,试求∠BOC的大小;
(2)若∠ABC和∠ACB的三等分线(即将一个角平均分成三等分的射线)相交于O,O1,如图2所示,试求∠BOC的大小;
(3)如此类推,若∠ABC和∠ACB的n等分线自下而上依次相交于O,O1,O2…,如图3所示,试探求∠BOC的大小与n的关系,并判断当∠BOC=170°时,是几等分线的交线所成的角.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com