
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(1,1),B(4,1),C(3,3).
(1)将△ABC向下平移5个单位后得到△A1B1C1,请画出△A1B1C1;
(2)将△ABC绕原点O逆时针旋转90°后得到△A2B2C2,请画出△A2B2C2;
(3)判断以O,A1,B为顶点的三角形的形状.(无须说明理由)

查看答案和解析>>
科目: 来源: 题型:
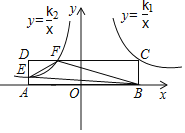
【题目】如图,矩形ABCD的顶点A,B在x轴上,且关于y轴对称,反比例函数y=![]() (x>0)的图象经过点C,反比例函数y=
(x>0)的图象经过点C,反比例函数y=![]() (x<0)的图象分别与AD,CD交于点E,F,若S△BEF=7,k1+3k2=0,则k1等于_____.
(x<0)的图象分别与AD,CD交于点E,F,若S△BEF=7,k1+3k2=0,则k1等于_____.
查看答案和解析>>
科目: 来源: 题型:
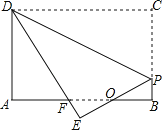
【题目】如图,矩形纸片ABCD,AB=4,BC=3,点P在BC边上,将△CDP沿DP折叠,点C落在点E处,PE、DE分别交AB于点O、F,且OP=OF,则cos∠ADF的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】某服装厂生产一种西装和领带,西装每套定价![]() 元,领带每条定价
元,领带每条定价![]() 元,厂方在开展促销活动期间,向客户提供两种优惠方案:
元,厂方在开展促销活动期间,向客户提供两种优惠方案:
①买一套西装送一条领带;
②西装和领带都按定价的![]() 付款.
付款.
现某客户要到该服装厂购买西装![]() 套,领带
套,领带![]() 条(
条(![]() ).
).
(1)客户分别按方案①、方案②购买,各需付款多少元?(用含![]() 的代数式表示);
的代数式表示);
(2)若![]() ,通过计算说明此时按哪种方案购买较为合算?
,通过计算说明此时按哪种方案购买较为合算?
查看答案和解析>>
科目: 来源: 题型:
【题目】一个自然数的立方,可以分裂成若干个连续奇数的和。例如:![]() 和
和![]() 分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即
分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即![]() =3+5;
=3+5;![]() =7+9+11;
=7+9+11;![]() =13+15+17+19;…;若
=13+15+17+19;…;若![]() 也按照此规律来进行“分裂”,则
也按照此规律来进行“分裂”,则![]() “分裂”出的奇数中,最大的奇数是______.
“分裂”出的奇数中,最大的奇数是______.

查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下面的情境对话,然后解答问题

(1)根据“奇异三角形”的定义,请你判断小华提出的命题:“等边三角形一定是奇异三角形”是真命题还是假命题?
(2)在Rt![]() ABC 中, ∠ACB=90°,AB=c,AC=b,BC=a,且b>a,若Rt
ABC 中, ∠ACB=90°,AB=c,AC=b,BC=a,且b>a,若Rt![]() ABC是奇异三角形,求a:b:c;
ABC是奇异三角形,求a:b:c;
(3)如图,AB是⊙O的直径,C是上一点(不与点A、B重合),D是半圆的中点,CD在直径AB的两侧,若在⊙O内存在点E使得AE=AD,CB=CE.
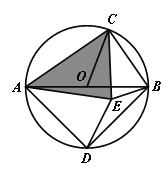
求证:![]() ACE是奇异三角形;
ACE是奇异三角形;
当![]() ACE是直角三角形时,求∠AOC的度数.
ACE是直角三角形时,求∠AOC的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.

(1)求证:BG=CF.
(2)请你判断BE+CF与EF的大小关系,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在正方形ABCD中,E是AD上一点,F是BA延长线上的一点,AF=AE,.
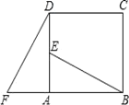
(1)求证:△ABE≌△ADF
(2)线段BE与DF有什么关系?证明你的结论.
查看答案和解析>>
科目: 来源: 题型:
【题目】数轴上![]() 点表示的数是
点表示的数是![]() ,
,![]() 点表示的数是
点表示的数是![]() ,则线段
,则线段![]() 的长表示为
的长表示为![]() .例如:数轴上
.例如:数轴上![]() 点表示的数是5,
点表示的数是5,![]() 点表示的数是2,则线段
点表示的数是2,则线段![]() 的长表示为
的长表示为![]() .
.
(1)点![]() 表示的数是3,线段
表示的数是3,线段![]() 的长可表示为______.
的长可表示为______.
(2)若![]() ,
,![]() ______.
______.
(3)数轴上的任意一点![]() 表示的数是
表示的数是![]() ,且
,且![]() 的最小值为5,若
的最小值为5,若![]() ,则
,则![]() 的值为______.
的值为______.
(4)如图,在数轴上点![]() 在点
在点![]() 的右边
的右边![]() ,
,![]() ,若代数式
,若代数式![]() 与
与![]() 互为相反数,求
互为相反数,求![]() 的值.
的值.
![]()
查看答案和解析>>
科目: 来源: 题型:
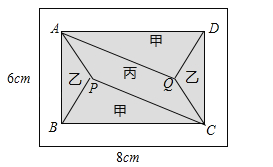
【题目】(2017浙江省温州市)小黄准备给长8m,宽6m的长方形客厅铺设瓷砖,现将其划分成一个长方形ABCD区域Ⅰ(阴影部分)和一个环形区域Ⅱ(空白部分),其中区域Ⅰ用甲、乙、丙三种瓷砖铺设,且满足PQ∥AD,如图所示.
(1)若区域Ⅰ的三种瓷砖均价为300元/m2,面积为S(m2),区域Ⅱ的瓷砖均价为200元/m2,且两区域的瓷砖总价为不超过12000元,求S的最大值;
(2)若区域Ⅰ满足BC=2:3,区域Ⅱ四周宽度相等.
①求AB,BC的长;
②若甲、丙两瓷砖单价之和为300元/m2,乙、丙瓷砖单价之比为5:3,且区域Ⅰ的三种瓷砖总价为4800元,求丙瓷砖单价的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com