
科目: 来源: 题型:
【题目】在矩形ABCD中,AD>AB,点P是CD边上的任意一点(不含C,D两端点),过点P作PF∥BC,交对角线BD于点F.
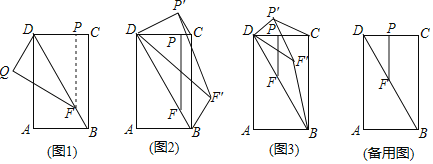
(1)如图1,将△PDF沿对角线BD翻折得到△QDF,QF交AD于点E.求证:△DEF是等腰三角形;
(2)如图2,将△PDF绕点D逆时针方向旋转得到△P'DF',连接P'C,F'B.设旋转角为α(0°<α<180°).
①若0°<α<∠BDC,即DF'在∠BDC的内部时,求证:△DP'C∽△DF'B.
②如图3,若点P是CD的中点,△DF'B能否为直角三角形?如果能,试求出此时tan∠DBF'的值,如果不能,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】松雷中学刚完成一批校舍的修建,有一些相同的办公室需要粉刷墙面.一天3名一级技工去粉刷7个办公室,结果其中有90m2墙面未来得及粉刷;同样时间内4名二级技工粉刷了7个办公室之外,还多粉刷了另外的70m2墙面.每名一级技工比二级技工一天多粉刷40m2墙面.
(1)求每个办公室需要粉刷的墙面面积.
(2)已知每名一级技工每天需要支付费用100元,每名二级技工每天需要支付费用90元.松雷中学有40个办公室的墙面和720m2的展览墙需要粉刷,现有3名一级技工的甲工程队,4名二级技工的乙工程队,要来粉刷墙面.松雷中学有两个选择方案,方案一:全部由甲工程队粉刷;方案二:全部由乙工程队粉刷;若使得总费用最少,松雷中学应如何选择方案,请通过计算说明.
查看答案和解析>>
科目: 来源: 题型:
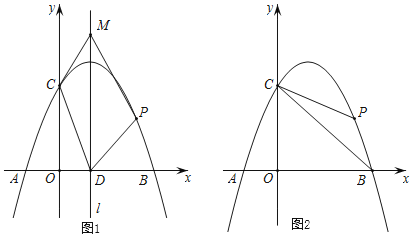
【题目】如图1,已知抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于C点,点P是抛物线上在第一象限内的一个动点,且点P的横坐标为t.
(1)求抛物线的表达式;
(2)设抛物线的对称轴为l,l与x轴的交点为D.在直线l上是否存在点M,使得四边形CDPM是平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.
(3)如图2,连接BC,PB,PC,设△PBC的面积为S.
①求S关于t的函数表达式;
②求P点到直线BC的距离的最大值,并求出此时点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】参照学习函数的过程与方法,探究函数y=![]() 的图象与性质.
的图象与性质.
因为y=![]() ,即y=﹣
,即y=﹣![]() +1,所以我们对比函数y=﹣
+1,所以我们对比函数y=﹣![]() 来探究.
来探究.
列表:
x | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | ﹣ |
| 1 | 2 | 3 | 4 | … |
y=﹣ | … |
|
| 1 | 2 | 4 | ﹣4 | ﹣1 | 1 | ﹣ | ﹣ | … |
y= | … |
|
| 2 | 3 | 5 | ﹣3 | ﹣1 | 0 |
|
| … |
描点:在平面直角坐标系中,以自变量x的取值为横坐标,以y=![]() 相应的函数值为纵坐标,描出相应的点,如图所示:
相应的函数值为纵坐标,描出相应的点,如图所示:
(1)请把y轴左边各点和右边各点,分别用一条光滑曲线顺次连接起来;
(2)观察图象并分析表格,回答下列问题:
①当x<0时,y随x的增大而 ;(填“增大”或“减小”)
②y=![]() 的图象是由y=﹣
的图象是由y=﹣![]() 的图象向 平移 个单位而得到;
的图象向 平移 个单位而得到;
③图象关于点 中心对称.(填点的坐标)
(3)设A(x1,y1),B(x2,y2)是函数y=![]() 的图象上的两点,且x1+x2=0,试求y1+y2+3的值.
的图象上的两点,且x1+x2=0,试求y1+y2+3的值.
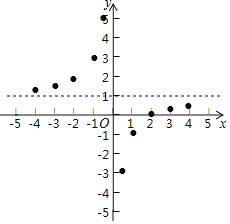
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线AB、CD相交于点O,过点O作两条射线OM、ON,且∠AOM=∠CON=90°

(1)若OC平分∠AOM,求∠AOD的度数.
(2)若∠1=![]() ∠BOC,求∠AOC和∠MOD.
∠BOC,求∠AOC和∠MOD.
查看答案和解析>>
科目: 来源: 题型:
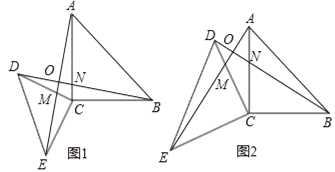
【题目】已知:△ACB和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,连接AE,BD交于点O,AE与DC交于点M,BD与AC交于点N.
(1)如图1,猜想AE与BD的数量关系与位置关系,并加以证明.
(2)如图2,若AC=DC,在不添加任何辅助线的情况下,请直接写出图2中四对全等的直角三角形.
查看答案和解析>>
科目: 来源: 题型:
【题目】某市为创建全国文明城市,开展“美化绿化城市”活动,计划经过若干年使城区绿化总面积新增360万平方米.自2013年初开始实施后,实际每年绿化面积是原计划的1.5倍,这样可提前4年完成任务.
(1)问实际每年绿化面积多少万平方米?
(2)为加大创城力度,市政府决定从2017年起加快绿化速度,要求不超过2年完成,那么实际平均每年绿化面积至少还要增加多少万平方米?
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两车站相距![]() ,一列慢车从甲站开出,每小时行驶
,一列慢车从甲站开出,每小时行驶![]() ,一列快车从乙站开出,每小时行驶
,一列快车从乙站开出,每小时行驶![]() .(必须用方程解,方程以外的方法不计分)
.(必须用方程解,方程以外的方法不计分)
(1)两车同时开出,相向而行,多少小时相遇?
(2)两车同时开出,同向而行,慢车在前,多少小时快车追上慢车?
查看答案和解析>>
科目: 来源: 题型:
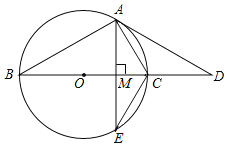
【题目】已知BC是⊙O的直径,点D是BC延长线上一点,AB=AD,AE是⊙O的弦,∠AEC=30°.
(1)求证:直线AD是⊙O的切线;
(2)若AE⊥BC,垂足为M,⊙O的半径为4,求AE的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】探究下面的问题:
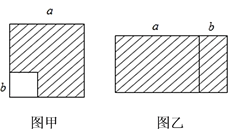
(1)如图甲,在边长为a的正方形中去掉一个边长为b的小正方形(a>b),把余下的部分剪拼成如图乙的一个长方形,通过计算两个图形(阴影部分)的面积,验证了一个等式,这个等式是________(用式子表示),即乘法公式中的___________公式.
(2)运用你所得到的公式计算:
①10.7×9.3
②![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com