(1)求△ABC的面积．

(2)△ABC中任意一点P(x0，y0)经平移后对应点为P1(x0+3，y0﹣4)，将△ABC作同样的平移得到△A1B1C1，写出A1、B1、C1的坐标．A1　 　，B1　 　，C1　 　．

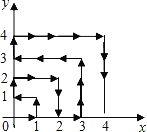
A.(4，45)B.(45，4)C.(44，4)D.(4，44)

（1）求y1的解析式；

（2）若y2随着x的增大而增大，且y1与y2都经过x轴上的同一点，求y2的解析式．

（1）(3分)求该反比例函数的解析式；

（2）(3分)将一次函数y=3x－2的图象向上平移4个单位，求平移后的图象与反比例函数图象的交点坐标；

（3）(2分)请直接写出一个同时满足如下条件的函数解析式：

①函数的图象能由一次函数y=3x－2的图象绕点（0，－2）旋转一定角度得到；

②函数的图象与反比例函数的图象没有公共点．

（1）两种机器人每小时分别搬运多少化工原料？

（2）该工厂原计划同时使用这两种机器人搬运，工作一段时间后，A型机器人又有了新的搬运任务，但必须保证这批化工原料在11小时内全部搬运完毕．求：A型机器人至少工作几个小时，才能保证这批化工原料在规定的时间内完成．

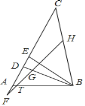
【题目】如图，在△ABC中，BD、BE分别是△ABC的高线和角平分线，点F在CA的延长线上，FH⊥BE交BD于点G，交BC于点H．下列结论：①∠DBE=∠F；②∠BEF=（∠BAF+∠C）； ③∠FGD=∠ABE+∠C；④∠F=（∠BAC﹣∠C）；其中正确的是_____．

（1）频数分布表中a=_____，b=_____，并将统计图补充完整；

（2）如果该校七年级共有女生180人，估计仰卧起坐能够一分钟完成30或30次以上的女学生有多少人？

（3）已知第一组中只有一个甲班学生，第四组中只有一个乙班学生，老师随机从这两个组中各选一名学生谈心得体会，则所选两人正好都是甲班学生的概率是多少？

A.1.16×1010B.11.6×109C.1.16×108D.1.6×109

【题目】已知：如图，直线y=kx+2与x轴正半轴相交于A（t，0），与y轴相交于点B，抛物线y=﹣x2+bx+c经过点A和点B，点C在第三象象限内，且AC⊥AB，tan∠ACB=．

（1）当t=1时，求抛物线的表达式；

（2）试用含t的代数式表示点C的坐标；

（3）如果点C在这条抛物线的对称轴上，求t的值．