
科目: 来源: 题型:
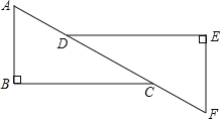
【题目】 如图,两块形状、大小完全相同的三角板按照如图所示的样子放置,找一找图中是否有互相平行的线段,完成下面证明:
证明:
∵∠______=∠______,
∴______∥______(______)(填推理的依据)
查看答案和解析>>
科目: 来源: 题型:
【题目】把下列各数分别填入相应的集合内:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (每两个
(每两个 ![]() 之间依次增加
之间依次增加 ![]() 个
个 ![]() ).
).
(1)正数集合:{ ┄};
(2)负数集合:{ ┄};
(3)整数集合:{ ┄};
(4)无理数集合:{ ┄}.
查看答案和解析>>
科目: 来源: 题型:
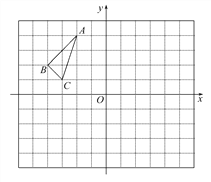
【题目】△ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.
(1)将△ABC向右平移2个单位长度,作出平移后的△A1B1C1,并写出△A1B1C1各顶点的坐标.
(2)若将△ABC绕点(-1,0)顺时针旋转180°后得到△A2B2C2,并写出△A2B2C2各顶点的坐标.
(3)观察△A1B1C1和△A2B2C2,它们是否关于某点成中心对称?若是,请写出对称中心的坐标;若不是,说明理由.
查看答案和解析>>
科目: 来源: 题型:
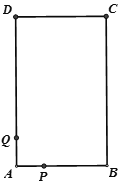
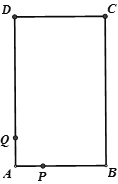
【题目】如图,长方形ABCD中,AB=4cm,BC=6cm,现有一动点P从A出发以2cm/秒的速度,沿矩形的边A—B—C—D回到点A,设点P的运动时间为t秒,
(1)当t=3秒时,求BP的长;
(2)当t为何值时,连接BP,AP,△ABP的面积为长方形的面积三分之一?
(3)Q为AD边上的点,且DQ=5,当t为何值时,以长方形的两个顶点及点P为顶点的三角形与△DCQ全等?
查看答案和解析>>
科目: 来源: 题型:
【题目】探索n×n的正方形钉子板上(n是钉子板每边上的钉子数,每边上相邻钉子间的距离为1),连接任意两个钉子所得到的不同长度值的线段种数:
当n=2时,钉子板上所连不同线段的长度值只有1与![]() ,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;
,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;
当n=3时,钉子板上所连不同线段的长度值只有1, ![]() ,2,
,2, ![]() ,2
,2![]() 五种,比n=2时增加了3种,即S=2+3=5.
五种,比n=2时增加了3种,即S=2+3=5.
(1)观察图形,填写下表:
钉子数(n×n) | S值 |
2×2 | 2 |
3×3 | 2+3 |
4×4 | 2+3+(____) |
5×5 | (________) |
(2)写出(n-1)×(n-1)和n×n的两个钉子板上,不同长度值的线段种数之间的关系;(用式子或语言表述均可).
(3)对n×n的钉子板,写出用n表示S的代数式.

查看答案和解析>>
科目: 来源: 题型:
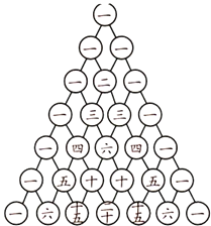
【题目】 我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”(如图)就是一例.这个三角形给出了(a+b)n(n=1,2,3,4,5,6)的展开式的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应(a+b)2=a2+2ab+b2展开式中各项的系数;第四行的四个数1,3,3,1,恰好对应着(a+b)3=a3+3a2b+3ab2+b3展开式中各项的系数,等等.
有如下四个结论:
①(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5;
②当a=-2,b=1时,代数式a3+3a2b+3ab2+b3的值是-1;
③当代数式a4+4a3b+6a2b2+4ab3+b4的值是0时,一定是a=-1,b=1;
④(a+b)n的展开式中的各项系数之和为2n.
上述结论中,正确的有______(写出序号即可).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知正方形ABCD的对角线交于O点,点E,F分别是AO,CO的中点,连接BE,BF,DE,DF,则下列结论中一定成立的是________.(把所有正确结论的序号都填在横线上)
①BF=DE;②∠ABO=2∠ABE;③S△AED=![]() S△ACD;④四边形BFDE是菱形.
S△ACD;④四边形BFDE是菱形.

查看答案和解析>>
科目: 来源: 题型:
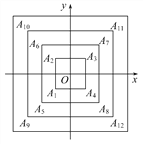
【题目】如图,正方形A1A2A3A4,A5A6A7A8,A9A10A11A12,…(每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为A1,A2,A3,A4;A5,A6,A7,A8;A9,A10,A11,A12;…)的中心均在坐标原点O,各边均与x轴或y轴平行,若它们的边长依次是2,4,6,…,则顶点A20的坐标为 ( )
A. (5,5) B. (5,-5) C. (-5,5) D. (-5,-5)
查看答案和解析>>
科目: 来源: 题型:
【题目】 在某次数学测试中,满分为100分,各测试内容及所占分值的分布情况如下扇形统计图,则以下结论正确的是( )
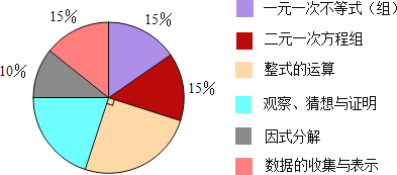
①一元一次不等式(组)部分与二元一次方程组部分所占分值一样
②因式分解部分在试卷上占10分
③整式的运算部分在整张试卷中所占比例为25%
④观察、猜想与证明部分的圆心角度数为72°
A.①②③B.②③④C.①④D.①②③④
查看答案和解析>>
科目: 来源: 题型:
【题目】下面是按规律排列的一列式子:
第1个式子:![]() ;
;
第2个式子: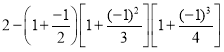 ;
;
第3个式子: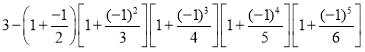 ;
;
……
(1)分别计算出这三个式子的结果;
(2)请按规律写出第2019个式子的形式(中间部分用省略号,两端部分必须写详细);
(3)计算第2019个式子的结果.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com